题目内容
（2012•驿城区模拟）如图，将一副三角板按如图方式叠放，则∠α等于75
75
°．分析：由于∠BAC=∠ACD=90°，那么∠BAC+∠ACD=180°，易证AB∥CD，于是可得∠1=∠B=45°，再利用三角形外角性质，可求∠α．
解答：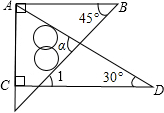
解：如图所示，
∵∠BAC=∠ACD=90°，
∴∠BAC+∠ACD=180°，
∴AB∥CD，
∴∠1=∠B=45°，
∴∠α=∠1+∠D=75°．
故答案是75°．
解：如图所示，∵∠BAC=∠ACD=90°，
∴∠BAC+∠ACD=180°，
∴AB∥CD，
∴∠1=∠B=45°，
∴∠α=∠1+∠D=75°．
故答案是75°．
点评：本题考查了三角形外角性质、平行线的判定和性质，解题的关键是先证明AB∥CD．
练习册系列答案
导学全程练创优训练系列答案
相关题目
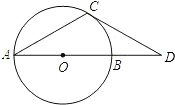（2012•驿城区模拟）如图，CD是⊙O的切线，D是直径AB的延长线上一点，∠D=30°，则∠BAC=
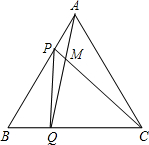（2012•驿城区模拟）如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s．