题目内容
已知三角形相邻两边长分别为20cm和30cm,第三边上的高为10cm,则此三角形的面积为分析:本题考虑两种情况,一种为相邻两边在高的两侧,一种为相邻两边在高的同侧,然后根据勾股定理求得第三边,从而求得三角形面积.
解答:解:设AB=30cm,AC=20cm,AD=10cm,
由题意作图,有两种情况: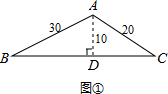
第一种:如图①,
在Rt△ABD中,利用勾股定理BD=
=
=20
cm,
同理求出CD=10
cm,
则三角形面积=
BC•AD=
(10
+20
)×10=(100
+50
)cm2
第二种:如图②,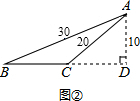
在Rt△ABD中,BD=
=
=20
cm
在Rt△ACD中,CD=
=
=10
cm
则BC=(20
-10
)cm
所以三角形面积=
BC•AD=
(20
-10
)×10=(100
-50
)cm2
故答案为:(100
+50
)或(100
-50
)
由题意作图,有两种情况:

第一种:如图①,
在Rt△ABD中,利用勾股定理BD=
| AB2-AD2 |
| 900-100 |
| 2 |
同理求出CD=10
| 3 |
则三角形面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
第二种:如图②,

在Rt△ABD中,BD=
| AB2-AD2 |
| 900-100 |
| 2 |
在Rt△ACD中,CD=
| AC2-AD2 |
| 400-100 |
| 3 |
则BC=(20
| 2 |
| 3 |
所以三角形面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:(100
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了勾股定理,两次运用勾股定理求出第三边,从两种情况来求第三边长,则再求三角形面积.

练习册系列答案
相关题目