Question

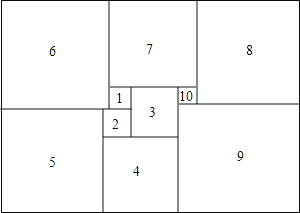
【题目】数学家莫伦在1925年发现了世界上第一个完美长方形．如图是一个完美长方形，它恰能被分割成10个大小不同的正方形，其中标注番号1的正方形边长为5，则这个完美长方形的面积为 ．

Answer 1

【答案】3055．

【解析】

试题分析：设标注番号2的正方形边长是x，根据各个正方形的边的和差关系分别表示出其余各正方形的边长，再根据完美长方形的宽相等列出方程，求解即可．

解：设标注番号2的正方形边长是x，标注番号1的正方形边长为5，

则第3个正方形的边长是x+5；

第4个正方形的边长是x+x+5=2x+5；

第5个正方形的边长是x+2x+5=3x+5；

第6个正方形的边长是3x+5+x﹣5=4x；

第7个正方形的边长是4x﹣5；

第10个正方形的边长是4x﹣5﹣5﹣（x+5）=3x﹣15；

第8个正方形的边长是4x﹣5+3x﹣15=7x﹣20；

第9个正方形的边长是3x﹣15+7x﹣20=10x﹣35；

根据题意得3x+5+4x=7x﹣20+10x﹣35，

解得x=6，

则完美长方形的宽为3x+5+4x=7x+5=47，

完美长方形的长为4x+4x﹣5+7x﹣20=15x﹣25=65，

所以完美长方形的面积为65×47=3055．

故答案为3055．