题目内容
在解方程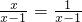
+1时，甲、乙两名同学的解法如下：
甲：原方程化为x=1+x-1，∴x=x，∴原方程的解为全体实数．
乙：原方程化为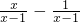
=1，∴
=1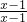．∴原方程的解为当x≠1时的任意实数．以下判断正确的是
- A.甲的解法正确，乙的解法错误
- B.甲的解法错误，乙的解法正确
- C.甲、乙的解法都正确
- D.甲、乙的解法都错误
B
分析：甲同学是按照解分式方程的一般方法做的，但是结果需要检验；甲错误．乙同学是直接通分，由除法的意义解题；乙正确．
解答：甲同学在方程两边乘（x-1）时，没有考虑到应该乘一个不为0的整式．如果结果检验可知原方程的解为当x≠1时的任意实数．故选B．
点评：当分式方程的两边乘整式的时候应该考虑所乘的整式不为0，分母不为0．
分析：甲同学是按照解分式方程的一般方法做的，但是结果需要检验；甲错误．乙同学是直接通分，由除法的意义解题；乙正确．
解答：甲同学在方程两边乘（x-1）时，没有考虑到应该乘一个不为0的整式．如果结果检验可知原方程的解为当x≠1时的任意实数．故选B．
点评：当分式方程的两边乘整式的时候应该考虑所乘的整式不为0，分母不为0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
－10x＋9=0
－10x＋9=0