题目内容
（2012•南岗区三模）在矩形ABCD中，连接AC，已知AD：AC=4：5，点E在CB的延长线上，连接AE，过点A作AF⊥AE交射线DC于点F．
（1）当点F在DC上时，如图1所示，求证：
BE+CF=AB；
（2）当点F在DC的延长线上时，如图2所示，AF交BC于点K，连接EF交射线AB于点G，将△ACF沿着直线AF翻折，翻折后直线AC交EF于点H，若AG=
，GF：AC=4
：7，求KH的长．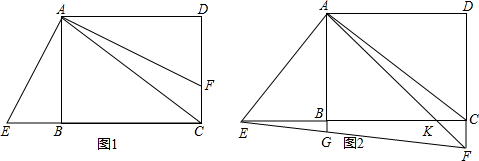
（1）当点F在DC上时，如图1所示，求证：
| 4 |
| 3 |
（2）当点F在DC的延长线上时，如图2所示，AF交BC于点K，连接EF交射线AB于点G，将△ACF沿着直线AF翻折，翻折后直线AC交EF于点H，若AG=
| 48 |
| 7 |
| 2 |
分析：（1）利用相似三角形的判定得出△ADF∽△ABE进而得出AD：AB=4：3，即可得出DF=
BE进而求出
BE+CF=AB；
（2）首先利用平行线的性质得出
=
=
，再证明△PAG∽△PEA，求出AE的长，进而得出△AOK∽△EOH和△AOE∽△KOH，得出∠AEO=∠KHO=45°，
在△AKH中，tan∠KAH=tan∠KEH=
=
=
=
，求出KN即可得出HK的长．
| 4 |
| 3 |
| 4 |
| 3 |
（2）首先利用平行线的性质得出
| GF |
| AC |
| PG |
| PA |
4
| ||
| 7 |
在△AKH中，tan∠KAH=tan∠KEH=
| BG |
| BE |
| KN |
| AN |
| ||
| 6 |
| 1 |
| 7 |
解答：解：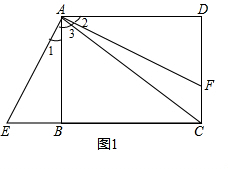
（1）∵AF⊥AE，
∴∠3+∠1=90°，
∵∠2+∠3=90°，
∴∠1=∠2，
∵∠D=∠ABE=90°，
∴△ADF∽△ABE，
∴
=
，
∵AD：AC=4：5，
∴AD：AB=4：3，
∴DF=
BE，
∵AB=CD，DF+FC=CD，
∴
BE+CF=AB；
（2）如图2，分别延长AC、EF交于点P，过点K作KN⊥AH于点N，
∵CF∥AG
∴
=
，
∵CF∥AG，
=
，
∴
=
=
，
由题知∠AEB+∠EAB=90°，∠KAB+∠EAB=90°
∴∠AEB=∠KAB
可得∠ACB=∠AFE，又∵∠AKC=∠EKF，
且∠CAK=180°-∠ACB-∠AKC，∠FEK=180°-∠AFE-∠EKF，
∴∠CAK=∠FEK
∴∠CAK+∠KAB=∠FEK+∠AEB，即∠PAG=∠PEA
又∵∠P=∠P
∴△PAG∽△PEA
∴
=
，
又∵
=
，
=
，
∵AG=
，
∴AE=6
，
在△AEG中，AE=6
，AG=
，tan∠AEG=
，可以得到∠EAB=45°，
∴AB=BE=6，BG=
，
由题意可知∠KAC=∠KAH，∴∠KAO=∠HEO
∵∠AOK=∠EOH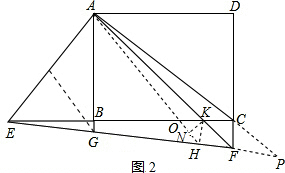
∴△AOK∽△EOH，∴∠EHO=∠AKO，且
=
，
=
，
又∠AOE=∠KOH，
∴△AOE∽△KOH，
∠AEO=∠KHO=45°，
在△AKH中，
tan∠KAH=tan∠KEH=
=
=
=
，
∵AK=6
，
∴设AN=7x，则KN=x，
则AK2=AN2+KN2，
即（6
）2=（7x）2+x2，
解得：x=
，
∵∠KHO=45°，∠KNH=90°，
则HK=
=
．
（1）∵AF⊥AE，∴∠3+∠1=90°，
∵∠2+∠3=90°，
∴∠1=∠2，
∵∠D=∠ABE=90°，
∴△ADF∽△ABE，
∴
| DF |
| EB |
| AD |
| AB |
∵AD：AC=4：5，
∴AD：AB=4：3，
∴DF=
| 4 |
| 3 |
∵AB=CD，DF+FC=CD，
∴
| 4 |
| 3 |
（2）如图2，分别延长AC、EF交于点P，过点K作KN⊥AH于点N，
∵CF∥AG
∴
| GF |
| AC |
| PF |
| PC |
∵CF∥AG，
| PF |
| PC |
| PG |
| PA |
∴
| GF |
| AC |
| PG |
| PA |
4
| ||
| 7 |
由题知∠AEB+∠EAB=90°，∠KAB+∠EAB=90°
∴∠AEB=∠KAB
可得∠ACB=∠AFE，又∵∠AKC=∠EKF，
且∠CAK=180°-∠ACB-∠AKC，∠FEK=180°-∠AFE-∠EKF，
∴∠CAK=∠FEK
∴∠CAK+∠KAB=∠FEK+∠AEB，即∠PAG=∠PEA
又∵∠P=∠P
∴△PAG∽△PEA
∴
| PG |
| PA |
| AG |
| AE |
又∵
| PG |
| PA |
4
| ||
| 7 |
| AG |
| AE |
4
| ||
| 7 |
∵AG=
| 48 |
| 7 |
∴AE=6
| 2 |
在△AEG中，AE=6
| 2 |
| 48 |
| 7 |
| 4 |
| 3 |
∴AB=BE=6，BG=
| 6 |
| 7 |
由题意可知∠KAC=∠KAH，∴∠KAO=∠HEO
∵∠AOK=∠EOH
∴△AOK∽△EOH，∴∠EHO=∠AKO，且
| AO |
| EO |
| KO |
| HO |
| AO |
| KO |
| EO |
| HO |
又∠AOE=∠KOH，
∴△AOE∽△KOH，
∠AEO=∠KHO=45°，
在△AKH中，
tan∠KAH=tan∠KEH=
| BG |
| BE |
| KN |
| AN |
| ||
| 6 |
| 1 |
| 7 |
∵AK=6
| 2 |
∴设AN=7x，则KN=x，
则AK2=AN2+KN2，
即（6
| 2 |
解得：x=
| 6 |
| 5 |
∵∠KHO=45°，∠KNH=90°，
则HK=
| KN |
| sin45° |
6
| ||
| 5 |
点评：此题主要考查了相似三角形的判定与性质以及锐角三角函数关系等知识，根据已知得出AK的长以及得出∠KHO=45°是解题关键．
练习册系列答案
相关题目
（2012•南岗区三模）如图，三角形纸片ABC中，∠B=2∠C，把三角形纸片沿直线AD折叠，点B落在AC边上的E处，那么下列等式成立的是（ ）
（2012•南岗区三模）如图，四边形ABCD中，AD∥BC，∠BCD的平分线CE⊥AB于点E，BE=2AE．若四边形AECD的面积为7，则四边形ABCD的面积为