题目内容
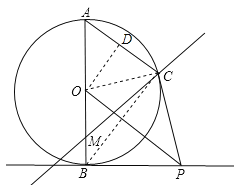
【题目】已知AB是⊙O的直径，PB是⊙O的切线，C是⊙O上的点，AC∥OP，M是直径AB上的动点，A与直线CM上的点连线距离的最小值为d，B与直线CM上的点连线距离的最小值为f．
（1）求证：PC是⊙O的切线；
（2）设OP=
AC，求∠CPO的正弦值；
（3）设AC=9，AB=15，求d+f的取值范围．
【答案】（1）证明见解析；（2）
；（3）9≤d+f≤15．
【解析】试题分析：（1）连接OC，根据等腰三角形的性质得到∠A=∠OCA，由平行线的性质得到∠A=∠BOP，∠ACO=∠COP，等量代换得到∠COP=∠BOP，由切线的性质得到∠OBP=90°，根据全等三角形的性质即可得到结论；
（2）过O作OD⊥AC于D，根据相似三角形的性质得到CDOP=OC2，根据已知条件得到
=
，由三角函数的定义即可得到结论；
（3）连接BC，根据勾股定理得到BC的值，当M与A重合时，得到d+f=12，当M与B重合时，得到d+f=9，于是得到结论．
试题解析：解：（1）连接OC，∵OA=OC，∴∠A=∠OCA，∵AC∥OP，∴∠A=∠BOP，∠ACO=∠COP，∴∠COP=∠BOP，∵PB是⊙O的切线，AB是⊙O的直径，∴∠OBP=90°，在△POC与△POB中，∵OC=OB，∠COP=∠BOP，OP=OP，∴△COP≌△BOP，∴∠OCP=∠OBP=90°，∴PC是⊙O的切线；
（2）过O作OD⊥AC于D，∴∠ODC=∠OCP=90°，CD=
AC，∵∠DCO=∠COP，∴△ODC∽△PCO，∴
，∴CDOP=OC2，∵OP=
AC，∴AC=
OP，∴CD=
OP，∴
OPOP=OC2，∴
=
，∴sin∠CPO=
=
；
（3）连接BC，∵AB是⊙O的直径，∴AC⊥BC，∵AC=9，AB=15，∴BC=
=12，当M与A重合时，d=0，f=AB=15，∴d+f=15，当M与B重合时，d=9，f=0，∴d+f=9，∴d+f的取值范围是：9≤d+f≤15．
