题目内容
(2006•武汉)(人教版)已知:二次函数y=x2-(m+1)x+m的图象交x轴于A(x1,0)、B(x2,0)两点,交y轴正半轴于点C,且x12+x22=10.(1)求此二次函数的解析式;
(2)是否存在过点D(0,-
 )的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求直线MN的解析式;若不存在,请说明理由.
)的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求直线MN的解析式;若不存在,请说明理由.
【答案】分析:(1)令y=0,即x2-(m+1)x+m=0,根据一元二次方程根与系数的关系及x12+x22=10,可求出m的值,再根据图象与y轴正半轴于点C,可求出函数的解析式;
(2)根据题意,设出一次函数解析式y=kx- ,若能求出比例系数,则可证明此直线存在.
,若能求出比例系数,则可证明此直线存在.
解答: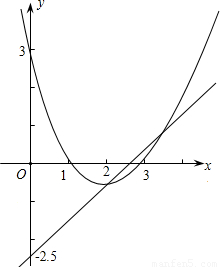 解:(1)因为x12+x22=10,
解:(1)因为x12+x22=10,
所以(x1+x2)2-2x1x2=10,根据根与系数的关系,(m+1)2-2m=10,
所以m=3,m=-3,
又因为点C在y轴的正半轴上,
∴m=3,
∴所求抛物线的解析式为:y=x2-4x+3;
(2)过点D(0,- )的直线与抛物线交于M(XM,YM)、N(XN,YN)两点,与x轴交于点E,使得M、N两点关于点E对称.
)的直线与抛物线交于M(XM,YM)、N(XN,YN)两点,与x轴交于点E,使得M、N两点关于点E对称.
设直线MN的解析式为:y=kx- ,
,
则有:YM+YN=0,(6分)
由 ,
,
x2-4x+3=kx- ,
,
移项后合并同类项得x2-(k+4)x+ =0,
=0,
∴xM+xN=4+k.
∴yM+yN=kxM- +kxN-
+kxN- =k(xM+xN)-5=0,
=k(xM+xN)-5=0,
∴yM+yN=k(xM+xN)=5,
即k(k+4)-5=0,
∴k=1或k=-5.
当k=-5时,方程x2-(k+4)x+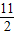 =0的判别式△<0,直线MN与抛物线无交点,
=0的判别式△<0,直线MN与抛物线无交点,
∴k=1,
∴直线MN的解析式为y=x- ,
,
∴此时直线过一、三、四象限,与抛物线有交点;
∴存在过点D(0, )的直线与抛物线于M,N两点,与x轴交于点E.使得M、N两点关于点E对称.
)的直线与抛物线于M,N两点,与x轴交于点E.使得M、N两点关于点E对称.
点评:此题巧妙利用了一元二次方程根与系数的关系.在(2)中,将直线与抛物线的交点问题转化为根与系数的关系解答,考查了同学们的整体思维能力.
(2)根据题意,设出一次函数解析式y=kx-
 ,若能求出比例系数,则可证明此直线存在.
,若能求出比例系数,则可证明此直线存在.解答:
 解:(1)因为x12+x22=10,
解:(1)因为x12+x22=10,所以(x1+x2)2-2x1x2=10,根据根与系数的关系,(m+1)2-2m=10,
所以m=3,m=-3,
又因为点C在y轴的正半轴上,
∴m=3,
∴所求抛物线的解析式为:y=x2-4x+3;
(2)过点D(0,-
 )的直线与抛物线交于M(XM,YM)、N(XN,YN)两点,与x轴交于点E,使得M、N两点关于点E对称.
)的直线与抛物线交于M(XM,YM)、N(XN,YN)两点,与x轴交于点E,使得M、N两点关于点E对称.设直线MN的解析式为:y=kx-
 ,
,则有:YM+YN=0,(6分)
由
 ,
,x2-4x+3=kx-
 ,
,移项后合并同类项得x2-(k+4)x+
 =0,
=0,∴xM+xN=4+k.
∴yM+yN=kxM-
 +kxN-
+kxN- =k(xM+xN)-5=0,
=k(xM+xN)-5=0,∴yM+yN=k(xM+xN)=5,
即k(k+4)-5=0,
∴k=1或k=-5.
当k=-5时,方程x2-(k+4)x+
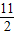 =0的判别式△<0,直线MN与抛物线无交点,
=0的判别式△<0,直线MN与抛物线无交点,∴k=1,
∴直线MN的解析式为y=x-
 ,
,∴此时直线过一、三、四象限,与抛物线有交点;
∴存在过点D(0,
 )的直线与抛物线于M,N两点,与x轴交于点E.使得M、N两点关于点E对称.
)的直线与抛物线于M,N两点,与x轴交于点E.使得M、N两点关于点E对称.点评:此题巧妙利用了一元二次方程根与系数的关系.在(2)中,将直线与抛物线的交点问题转化为根与系数的关系解答,考查了同学们的整体思维能力.

练习册系列答案
相关题目
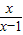 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )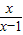 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )