题目内容
已知函数:①y=2x2-| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
分析:因为⑥y=x2+4x+4=(x+2)2,其它几个函数都是顶点式,写出每个函数的顶点坐标及对称轴,直接判断.
解答:解:①y=2x2-
,顶点坐标是(0,-
),对称轴是直线x=0(y轴);
②y=2x2-
,顶点坐标是(0,-
),对称轴是直线x=0(y轴);
③y=x2,顶点坐标是(0,0),对称轴是直线x=0(y轴);
④y=-2(x-
)2,顶点坐标是(-
,0),对称轴是直线x=-
;
⑤y=x2-2,顶点坐标是(0,-2),对称轴是直线x=0(y轴);
⑥y=x2+4x+4=(x+2)2,顶点坐标是(-2,0),对称轴是直线x=-2.
可知:图象顶点在原点的是③;图象顶点在x轴上的是③④⑥;图象对称轴是y轴所在直线的是①②③⑤.
| 3 |
| 2 |
| 3 |
| 2 |
②y=2x2-
| 1 |
| 2 |
| 1 |
| 2 |
③y=x2,顶点坐标是(0,0),对称轴是直线x=0(y轴);
④y=-2(x-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
⑤y=x2-2,顶点坐标是(0,-2),对称轴是直线x=0(y轴);
⑥y=x2+4x+4=(x+2)2,顶点坐标是(-2,0),对称轴是直线x=-2.
可知:图象顶点在原点的是③;图象顶点在x轴上的是③④⑥;图象对称轴是y轴所在直线的是①②③⑤.
点评:求抛物线的顶点坐标、对称轴及最值通常有两种方法:
(1)公式法:y=ax2+bx+c的顶点坐标为(-
,
),对称轴是x=-
;
(2)配方法:将解析式化为顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.
(1)公式法:y=ax2+bx+c的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
(2)配方法:将解析式化为顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是x=h.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知函数:①y=2x;②y=2+5x;③y=
(x>0);④y=
;⑤y=
,其中y随着x的增大而增大的有( )
| -3 |
| x |
| 5 |
| x |
| k2+2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
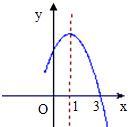 9、已知函数y=-x2+2x+c的部分图象如图所示,若y≤0,则x的取值范围是( )
9、已知函数y=-x2+2x+c的部分图象如图所示,若y≤0,则x的取值范围是( ) 已知函数y=-x2+2x+c的部分图象如图所示,则c=
已知函数y=-x2+2x+c的部分图象如图所示,则c=