题目内容
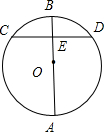如图：AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10cm，CD=8cm，那么AE的长为（ ）| A、5cm | B、4cm | C、3cm | D、8cm |
分析：连接OC，已知直径和弦长，利用勾股定理可以求出OE，从而确定AE．
解答：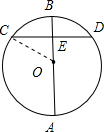
解：连接OC，
∵弦CD⊥AB，
∴CE=DE，
∵CD=8cm，
∴CE=DE=4cm，
在Rt△OCE中，
∵AB=10cm，
∴OC=5cm，
∴OE=
=3，
所以AE=AO+OE=5+3=8．
故选D．
解：连接OC，∵弦CD⊥AB，
∴CE=DE，
∵CD=8cm，
∴CE=DE=4cm，
在Rt△OCE中，
∵AB=10cm，
∴OC=5cm，
∴OE=
| 52-42 |
所以AE=AO+OE=5+3=8．
故选D．
点评：解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r，弦长为a，这条弦的弦心距为d，则有等式r2=d2+（
）2成立，知道这三个量中的任意两个，就可以求出另外一个．
| a |
| 2 |
练习册系列答案
相关题目
8、如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为（ ）
0.1平方米）
如图，AB是铅直地竖立在坡角为30°的山坡上的电线杆，当阳光与水平线成60°角时，电线杆的影子BC的长度为4米，则电线杆AB的高度为