题目内容
如图，∠B=40°，∠C=60°，AF、AD分别是△ABC的角平分线和高，
求：（1）∠BAC的度数；
（2）∠DAF的度数。
求：（1）∠BAC的度数；
（2）∠DAF的度数。
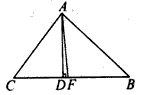
解：（1）∠BAC=180°-∠B-∠C=180°-40°-60°=80°；
（2）因为AF平分∠CAB，
∠CAF=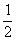
×80°=40°，
因为AD是△ABC的高，
所以∠CDA=90°，
∠CAD=180°-∠C-∠CDA=180°-60°-90°=30°，
所以∠DAF=∠CAF -∠CAD=40°-30°=10°。
（2）因为AF平分∠CAB，
∠CAF=
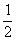×80°=40°，因为AD是△ABC的高，
所以∠CDA=90°，
∠CAD=180°-∠C-∠CDA=180°-60°-90°=30°，
所以∠DAF=∠CAF -∠CAD=40°-30°=10°。
练习册系列答案
相关题目
如图，∠ABC=40°，∠ACB=60°，BO、CO平分∠ABC和∠ACB，DE过O点，且DE∥BC，则∠BOC=
24、已知：如图，∠1=40°，∠2=65°，AB∥DC，求：∠ADC和∠A的度数．
程．公司通过销售记录发现，前20天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．
20、如图，∠AOB=40°，边OA为平面镜，在OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行．则∠QPB的度数为
如图，∠AOB=40°，PC⊥OA于C，PD⊥OB于D，且PC=PD，则∠OPC=