题目内容
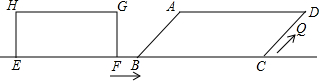
(2009•邯郸二模)如图,矩形EFGH的边EF=6cm,EH=3cm,在平行四边形ABCD中,BC=10cm,AB=5cm,sin∠ABC=
,点EFBC在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右移动,当D点落在边CF所在直线上即停止.
(1)在矩形运动过程中,何时矩形的一边恰好通过平行四边形的边AB或CD的中点?
(2)在矩形运动过程中,当矩形与平行四边形重叠部分为五边形时,求出重叠面积S(cm2)与运动时间t(s)之间的函数关系式,并写出时间t的范围.是否存在某一时刻,使得重叠部分的面积S=16.5cm2?若存在,求出时间t,若不存在,说明理由.(3)若矩形运动的同时,点Q从点C出发沿C-D-A-B的路线,以0.5cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在进行一边上运动的时间为多少s?
| 3 | 5 |
(1)在矩形运动过程中,何时矩形的一边恰好通过平行四边形的边AB或CD的中点?
(2)在矩形运动过程中,当矩形与平行四边形重叠部分为五边形时,求出重叠面积S(cm2)与运动时间t(s)之间的函数关系式,并写出时间t的范围.是否存在某一时刻,使得重叠部分的面积S=16.5cm2?若存在,求出时间t,若不存在,说明理由.(3)若矩形运动的同时,点Q从点C出发沿C-D-A-B的路线,以0.5cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在进行一边上运动的时间为多少s?

分析:(1)何时矩形的一边恰好通过?ABCD的边AB或CD的中点,题目本身就不明确,到底是GF还是HE,经过了AB的中点还是CD的中点,所以必须分情况讨论,即①当GF边通过AB边的中点②当EH边通过AB边的中点③当GF边通过CD边的中点
(2)设当矩形运动到t(s)(7<t<11)时与平行四边形的重叠部分为五边形,则BE、AH都可用含有t的式子表示出来.在矩形EFGH中易证△AHP∽△BEP根据对应线段成比例,可求出EP的长,因此面积可表示出来.
(3)点Q在矩形一边上运动的时间为多少s,这里的“一边”是哪一边,必须分情况进行解释,所以也有三种情况.
(2)设当矩形运动到t(s)(7<t<11)时与平行四边形的重叠部分为五边形,则BE、AH都可用含有t的式子表示出来.在矩形EFGH中易证△AHP∽△BEP根据对应线段成比例,可求出EP的长,因此面积可表示出来.
(3)点Q在矩形一边上运动的时间为多少s,这里的“一边”是哪一边,必须分情况进行解释,所以也有三种情况.
解答:解:(1)作AM⊥BC,∵AB=5,sin∠ABC=3/5,
∴BM=4,AM=3,
①当GF边通过AB边的中点N时,
有BF=
BM=2,
∴t1=3(s).
②当EH边通过AB边的中点N时,
有BE=
BM=2,
∴BF=2+6=8,
∴t2=8+1=9(s).
③当GF边通过CD边的中点K时,
有CF=2,
∴t3=1+10+2=13(s),
综上,当t等于3s或9s或13s时,矩形的一边恰好通过平行四边形的边AB或CD的中点.
(2)设当矩形运动到t(s)(7<t<11)时与平行四边形的重叠部分为五边形,
则BE=t-7,AH=4-(t-7)=11-t,
在矩形EFGH中,有AH∥BF,
∴△AHP∽△BEP,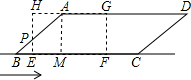
∴
=
,
∴
=
,
∴EP=
,
∴S=18-
(11-t)×
,
=-
(t-11)2+18(7<t<11),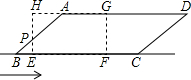
由对称性知当11<t<15时重叠部分仍为五边形,
综上S与t的函数关系式为:S=-
(t-11)2+18(7<t<15且t≠11),
把s=16.5代入得:16.5=-
(t-11)2+18,
∴t1=9,t2=13,
即当t等于9s或13s时重叠部分的面积为16.5cm2.
(3)点Q从点C运动到点D所需的时间为:
5÷(
)=10(s),
此时,DG=1+14-10=5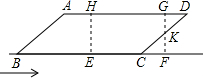 ,
,
点Q从D点运动开始到与矩形相遇所需的时间为:
=
,
∴矩形从与点Q相遇到运动到停止所需的时间为:5-
=
,
从相遇到停止点Q运动的路程为:
×
=
,
+
=
<6,
即点Q从相遇到停止一直在矩形的边GH上运动,
∴点Q在矩形的一边上运动的时间为:
s.
∴BM=4,AM=3,
①当GF边通过AB边的中点N时,
有BF=
| 1 |
| 2 |
∴t1=3(s).
②当EH边通过AB边的中点N时,
有BE=
| 1 |
| 2 |
∴BF=2+6=8,
∴t2=8+1=9(s).
③当GF边通过CD边的中点K时,
有CF=2,
∴t3=1+10+2=13(s),
综上,当t等于3s或9s或13s时,矩形的一边恰好通过平行四边形的边AB或CD的中点.
(2)设当矩形运动到t(s)(7<t<11)时与平行四边形的重叠部分为五边形,
则BE=t-7,AH=4-(t-7)=11-t,
在矩形EFGH中,有AH∥BF,
∴△AHP∽△BEP,

∴
| BE |
| HA |
| PE |
| PH |
∴
| 11-t |
| t-7 |
| EP |
| 3-EP |
∴EP=
| 3(11-t) |
| 4 |
∴S=18-
| 1 |
| 2 |
| 3(11-t) |
| 4 |
=-
| 3 |
| 8 |

由对称性知当11<t<15时重叠部分仍为五边形,
综上S与t的函数关系式为:S=-
| 3 |
| 8 |
把s=16.5代入得:16.5=-
| 3 |
| 8 |
∴t1=9,t2=13,
即当t等于9s或13s时重叠部分的面积为16.5cm2.
(3)点Q从点C运动到点D所需的时间为:
5÷(
| 1 |
| 2 |
此时,DG=1+14-10=5
 ,
,点Q从D点运动开始到与矩形相遇所需的时间为:
| 5 | ||
1+
|
| 10 |
| 3 |
∴矩形从与点Q相遇到运动到停止所需的时间为:5-
| 10 |
| 3 |
| 5 |
| 3 |
从相遇到停止点Q运动的路程为:
| 1 |
| 2 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 3 |
| 5 |
| 2 |
即点Q从相遇到停止一直在矩形的边GH上运动,
∴点Q在矩形的一边上运动的时间为:
| 5 |
| 3 |
点评:此题主要考查了矩形的性质,此题在解答过程中,一定要注意分情况讨论,另外还考查了二次函数的一些基本应用,考查比较全面,难易程度适中.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
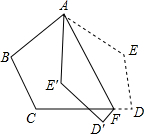 (2009•邯郸二模)将五边形ABCDE按如图方式折叠,折痕为AF.点E、D分别落在E′,D′.已知∠AFC=76°,则∠CFD′=
(2009•邯郸二模)将五边形ABCDE按如图方式折叠,折痕为AF.点E、D分别落在E′,D′.已知∠AFC=76°,则∠CFD′=