题目内容
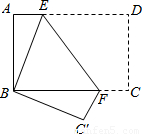
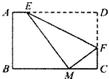20、如图所示，在矩形纸片ABCD中，已知AB：BC=2：3，点M在BC边上，将矩形折叠，使点D落在点M处，折痕为EF，若AE=2，CM=4，则AB的长为8
．分析：根据题意已知AB：BC=2：3，可用x表示出AB、BC的长，再利用辅助线及勾股定理解出x，从而求出AB的长．
解答：解：从E点向BC边做垂直线EG，
由题意可知AB：BC=2：3，可设AB=2x，BC=3x，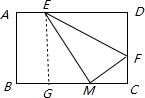
可知EG=2x，GM=3x-6，EM=3x-2，
根据勾股定理EG2+GM2=EM2
可得x=4，x=2，
∴x≠2，
故结果为AB边长为8．
故答案为：8．
由题意可知AB：BC=2：3，可设AB=2x，BC=3x，
可知EG=2x，GM=3x-6，EM=3x-2，
根据勾股定理EG2+GM2=EM2
可得x=4，x=2，
∴x≠2，
故结果为AB边长为8．
故答案为：8．
点评：此题主要考查勾股定理的应用，要学会作辅助线，构造直角三角形，从而求解．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
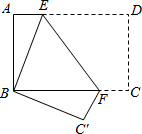8、如图所示，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF，若∠EFC′=125°，那么∠ABE的度数为（ ）
D按如下顺序进行折叠：对折，展平，得折痕EF（如图①）；沿CG折叠，使点B落在EF上的点B′处，（如图②）；展平，得折痕GC（如图③）；沿GH折叠，使点C落在DH上的点C′处，（如图④）；沿GC′折叠（如图
′是正三角形吗？请说明理由．
