题目内容
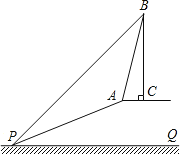
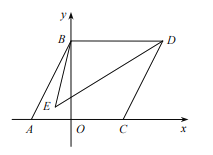
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,将线段
,将线段![]() 沿着
沿着![]() 轴向右平移至
轴向右平移至![]() ,使点
,使点![]() 与点
与点![]() 对应,点
对应,点![]() 与点
与点![]() 对应,连接
对应,连接![]() .
.
(1)若![]() ,
,![]() 满足
满足![]() .
.
①填空:![]() _______,
_______,![]() _______;
_______;
②若面积关系![]() 成立,则点
成立,则点![]() 的坐标为_______;
的坐标为_______;
(2)![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,判断
,判断![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)①![]() ②D(8,8)(2)45°
②D(8,8)(2)45°
【解析】
(1)①根据非负数相加等于零,可知它们本身等于零,即可得出答案.
②根据“![]() ”可得四边形OCDB的面积,再根据BD=AC,进而得出OC=4,所以BD=8即可得出坐标
”可得四边形OCDB的面积,再根据BD=AC,进而得出OC=4,所以BD=8即可得出坐标
(2)根据平行线的性质可知∠ABE=∠BEF,∠FED=∠EDC,∠ABD+∠BDC=180°,再根据“![]() 平分
平分![]() ,
,![]() 平分
平分![]() ”,即可得出结论
”,即可得出结论
(1)①∵![]()
∴![]()
∴![]()
②∵点![]() ,
,![]()
∴OA=![]() ,OB=8
,OB=8
∵ ![]()
∴![]() =48
=48
∵由题意可知BD=AC
∴![]()
∴OC=4
∴BD=8
∴D(8,8)
(2)
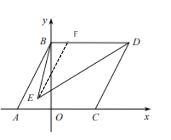
过E 作EF∥BA交BD于F点
由题意可知EF∥BA∥DC
∴∠ABE=∠BEF,∠FED=∠EDC,∠ABD+∠BDC=180°
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]()
∴∠ABE=![]() ∠ABO,∠EDC=
∠ABO,∠EDC=![]() ∠BDC
∠BDC
∴∠BED=![]() =
=![]()

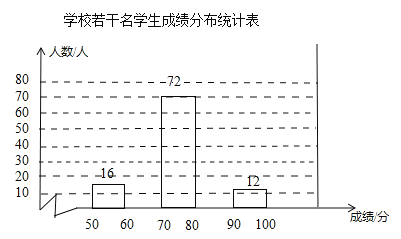
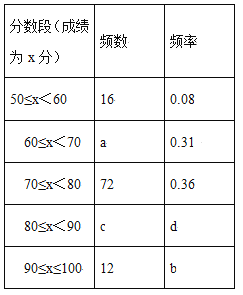
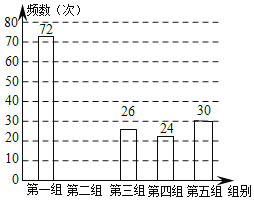
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)