题目内容

如图，△ABC中，AB=AC=18，BC=12，正方形DEFG的顶点E，F在△ABC内，顶点D，G分别在AB，AC上，AD=AG，DG=6，则点F到BC的距离为（　　）
A、1
B、2
C、12
2
-6
D、6
2
-6
练习册系列答案
相关题目
如图，抛物线y=-x2-4x+c（c＜0）与x轴交于点A和点B（n，0），点A在点B的左侧，则AB的长是（　　）
A、4-2nB、4+2nC、8-2nD、8+2n
如图，已知∠1=∠2，若再增加一个条件不一定能使结论△ADE∽△ABC成立，则这个条件是（　　）
A、∠D=∠B
B、∠AED=∠C
C、
AD
AB
=
AE
AC
D、
AD
AB
=
DE
BC
若△ABC∽△A1B1C1（其中点A和A1、B和B1、C和C1分别对应），且AB=4，A1 B1=6，则△ABC的周长和△A1B1C1的周长之比是（　　）
A、9：4B、4：9C、2：3D、3：2
如图，在△ABC中，点D在边AB上，BD=2AD，DE∥BC交AC于点E，若线段DE=5，则线段BC的长为（　　）
A、7.5B、10C、15D、20
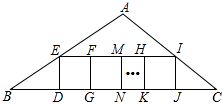如图，已知△ABC的面积是12，BC=6，点E、I分别在边AB、AC上，在BC边上依次做了n个全等的小正方形DEFG，GFMN，…，KHIJ，则每个小正方形的边长为（　　）
A、
12
11
B、
12
2n-3
C、
12
5
D、
12
2n+3
如图，在正方形ABCD中，E为AB的中点，G，F分别为AD，BC边上的点，若AG=1，BF=2，∠GEF=90°，则GF的长为（　　）
A、xB、2C、nD、3
如图，已知第一象限内的点A在反比例函数y=
2
x
的图象上，第二象限内的点B在反比例函数y=
k
x
的图象上，且OA⊥OB，cosA=0.5，则k的值为（　　）
A、-3
B、-6
C、-
3
D、-2
3
在Rt△ABC中，∠C=90°，若AB=2，AC=1，则tanA的值为（　　）
A、
1
2
B、
3
2
C、
3
3
D、
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网