题目内容
设圆心P的坐标为(-| 1 | sin30° |
分析:先将sin30°=
,tan60°=
,cot45°=1代入,求出点P和点A的坐标,从而得出半径PA的长,然后和点P的纵坐标比较即可.
| 1 |
| 2 |
| 3 |
解答:解:由题意得:点P的坐标为(-3,-
),点A的坐标为(-2,0),
∴r=PA=
=2,
因为点P的横坐标为-3,到y轴的距离为d=3>2,
∴⊙P与y轴的位置关系是相离.
| 3 |
∴r=PA=
(-1)2+(
|
因为点P的横坐标为-3,到y轴的距离为d=3>2,
∴⊙P与y轴的位置关系是相离.
点评:本题考查直线与圆的位置关系,本题的关键之处在于利用两点间的距离公式求出半径的长,然后根据d<r,相交;d=r,相切,d>r相离进行判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =-x2+bx+c的图象经过A、B两点,其顶点为F.
=-x2+bx+c的图象经过A、B两点,其顶点为F. 如图,抛物线y=x2-2x+k与x轴交于A、B两点,与y轴交于点C(0,-3).
如图,抛物线y=x2-2x+k与x轴交于A、B两点,与y轴交于点C(0,-3).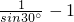 ,-tan60°),点A(-2cot45°,0)在⊙P上,试判别⊙P与y轴的位置关系.
,-tan60°),点A(-2cot45°,0)在⊙P上,试判别⊙P与y轴的位置关系.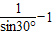 ,-tan60°),点A(-2cot45°,0)在⊙P上,试判别⊙P与y轴的位置关系.
,-tan60°),点A(-2cot45°,0)在⊙P上,试判别⊙P与y轴的位置关系.