题目内容
(2010•大连二模)如图,△ABC内接于⊙O,AB是直径,点D是弧BC的中点,连接AD,交BC于点F.(1)过点D作DE∥BC,交AC的延长线于点E,判断DE是否是⊙O的切线,并说明理由;
(2)若CD=6,AC:AF=4:5,求⊙O的半径.

【答案】分析:(1)连接OD、BD,先由OA=OD,可得∠OAD=∠ODA,而D是弧BC的中点,那么弧CD=弧BD,利用同圆中相等的弧所对的圆周角相等,可得∠BAD=∠CAD,从而∠ODA=∠CAD,利用内错角相等两直线平行,可知OD∥AC,再利用平行线的性质有∠AED+∠ODE=180°,由于AB是直径,就有∠ACB=90°,而BC∥DE,那么∠AED=∠ACB=90°,代入∠AED+∠ODE=180°中,可求∠ODE=90°,即DE是⊙O的切线;
(2)由于AB是直径,那么∠ADB=∠ACB=90°,由(1)可知∠CAD=∠BAD,所以就有△ACF≌△ADB,可得比例线段AD:AB=AC:AF=4:5,于是有cos∠BAD= ,可求sin∠BAD=
,可求sin∠BAD= ,而sin∠BAD=BD:AB,又BD=CD=6,于是可求AB=10,则半径=5.
,而sin∠BAD=BD:AB,又BD=CD=6,于是可求AB=10,则半径=5.
解答:解: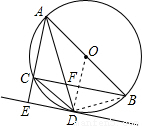 (1)DE是⊙O的切线.(说明:结论(1分),但不重复得分)
(1)DE是⊙O的切线.(说明:结论(1分),但不重复得分)
证明:连接OD、BD,
∵OA=OD,
∴∠ODA=∠OAD,(1分)
∵点D是弧BC的中点,
∴弧DC=弧BD,
∴∠CAD=∠OAD,(2分)
∴∠CAD=∠ODA,
∴OD∥AC,(3分)
∴∠ODE+∠AED=180°,
∵AB是直径,
∴∠ACB=90°,(4分)
又∵DE∥BC,
∴∠AED=∠ACB=90°,
∴∠ODE=90°,
∴OD⊥DE,(5分)
∴DE是⊙O的切线.(6分)
(2)∵AB是直径,
∴∠ADB=∠ACB=90°(7分)
由(1)知,∠CAD=∠BAD,
∴△ACF∽△ADB,(8分)
∴ ,
,
∴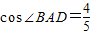 ,
,
∴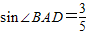 ,
,
又∵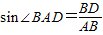 ,BD=CD=6,
,BD=CD=6,
∴AB=10,(9分)
∵AB是⊙O直径,
∴⊙O的半径为5.(10分)
点评:本题主要考查了同圆中相等的弧所对的圆周角相等、平行线的判定和性质、切线的判定、直径所对的圆周角等于90°、相似三角形的判定和性质、三角函数值.
(2)由于AB是直径,那么∠ADB=∠ACB=90°,由(1)可知∠CAD=∠BAD,所以就有△ACF≌△ADB,可得比例线段AD:AB=AC:AF=4:5,于是有cos∠BAD=
 ,可求sin∠BAD=
,可求sin∠BAD= ,而sin∠BAD=BD:AB,又BD=CD=6,于是可求AB=10,则半径=5.
,而sin∠BAD=BD:AB,又BD=CD=6,于是可求AB=10,则半径=5.解答:解:
 (1)DE是⊙O的切线.(说明:结论(1分),但不重复得分)
(1)DE是⊙O的切线.(说明:结论(1分),但不重复得分)证明:连接OD、BD,
∵OA=OD,
∴∠ODA=∠OAD,(1分)
∵点D是弧BC的中点,
∴弧DC=弧BD,
∴∠CAD=∠OAD,(2分)
∴∠CAD=∠ODA,
∴OD∥AC,(3分)
∴∠ODE+∠AED=180°,
∵AB是直径,
∴∠ACB=90°,(4分)
又∵DE∥BC,
∴∠AED=∠ACB=90°,
∴∠ODE=90°,
∴OD⊥DE,(5分)
∴DE是⊙O的切线.(6分)
(2)∵AB是直径,
∴∠ADB=∠ACB=90°(7分)
由(1)知,∠CAD=∠BAD,
∴△ACF∽△ADB,(8分)
∴
 ,
,∴
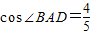 ,
,∴
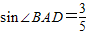 ,
,又∵
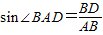 ,BD=CD=6,
,BD=CD=6,∴AB=10,(9分)
∵AB是⊙O直径,
∴⊙O的半径为5.(10分)
点评:本题主要考查了同圆中相等的弧所对的圆周角相等、平行线的判定和性质、切线的判定、直径所对的圆周角等于90°、相似三角形的判定和性质、三角函数值.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 的值,其中
的值,其中