题目内容
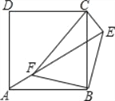
如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．
（1）求证：△ABF≌△CBE；
（2）判断△CEF的形状，并说明理由．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
轻松课堂单元期中期末专题冲刺100分系列答案题目内容
如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．
（1）求证：△ABF≌△CBE；
（2）判断△CEF的形状，并说明理由．
轻松课堂单元期中期末专题冲刺100分系列答案
的图象是抛物线，则
等于（ ）
，这里“∑”是求和符号通过对以上材料的阅读，计算
= ．
B. 
D. 
的解是
________；
________．