题目内容
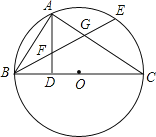
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
【答案】(1)证明见解析;(2)![]() π.
π.
【解析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵![]() =
=![]() ,
,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵![]() =
=![]() ,
,
∴∠AOE=60°.
∴∠EOC=60°.
∴![]() 的长为2π×(2+2)×
的长为2π×(2+2)×![]() =
=![]() π.
π.

练习册系列答案
相关题目