题目内容
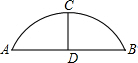 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为________米.
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为________米.
8
分析:先构建直角三角形,再利用勾股定理和垂径定理计算.
解答: 解:因为跨度AB=24m,拱所在圆半径为13m,
解:因为跨度AB=24m,拱所在圆半径为13m,
延长CD到O,使得OC=OA,则O为圆心,
则AD= AB=12(米),
AB=12(米),
则OA=13米,
在Rt△AOD中,DO=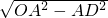 =5,
=5,
进而得拱高CD=CO-DO=13-5=8米.
故答案为:8.
点评:本题主要考查直角三角形和垂径定理的应用,根据题意作出辅助线是解答此题的关键.
分析:先构建直角三角形,再利用勾股定理和垂径定理计算.
解答:
 解:因为跨度AB=24m,拱所在圆半径为13m,
解:因为跨度AB=24m,拱所在圆半径为13m,延长CD到O,使得OC=OA,则O为圆心,
则AD=
 AB=12(米),
AB=12(米),则OA=13米,
在Rt△AOD中,DO=
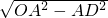 =5,
=5,进而得拱高CD=CO-DO=13-5=8米.
故答案为:8.
点评:本题主要考查直角三角形和垂径定理的应用,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
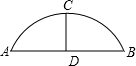 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )| A、5米 | ||
| B、8米 | ||
| C、7米 | ||
D、5
|
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度AB为24米,拱的半径为13米,则拱高CD为( )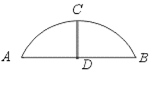
| A.5米 | B.7米 | C.5 米 米 | D.8米. |

 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱高为8米,则圆弧半径为
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱高为8米,则圆弧半径为
 米
C.7米 D. 8米
米
C.7米 D. 8米