题目内容
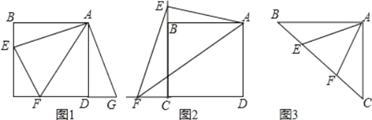
【题目】如图,矩形纸片![]() ,对角线为
,对角线为![]() ,沿过点
,沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() ,若
,若![]() ,则
,则![]() 的长是( )
的长是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由折叠即可得∠GDA=∠GDB,AD=ED,然后过点G作GE⊥BD于E,即可得AG=EG,设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,在Rt△BEG中利用勾股定理,即可求得AG的长.
根据题意可得:∠GDA=∠GDB,AD=ED,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3,
∴AG=EG,ED=3,
∵AB=4,BC=3,∠A=90°,
∴BD=5,
设AG=x,则GE=x,BE=BD-DE=5-3=2,BG=AB-AG=4-x,
在Rt△BEG中,EG2+BE2=BG2,
即:x2+4=(4-x)2,
解得:x=![]() ,
,
∴AG=![]() .
.
故选:B.

练习册系列答案
相关题目
【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
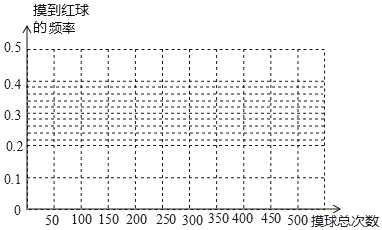
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).