题目内容
(2004•泸州)如图,半径为6.5的⊙O′经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+60=0的两根.(1)求A、B两点的距离;
(2)求点A和点B的坐标;
(3)已知点C在劣弧OA上,连接BC交OA于D,当OC2=CD•BC时,求点C的坐标;
(4)在⊙O′上是否存在点P,使△ABD的面积等于△POD的面积,即S△ABD=S△POD?若存在,请求出点P的坐标;如果不存在,请说明理由.注:抛物线y=ax2+bx+c(a≠0)的顶点为(-
 )
)
【答案】分析:(1)由于∠BOA=90°,根据圆周角定理可知:AB的长即为圆的直径;
(2)可在直角三角形OBA中,根据勾股定理和韦达定理来求出OA,OB的长;
(3)已知了OC2=CD•BC,那么三角形OCD和BCO相似,因此∠OBC=∠DOC,此时可得出弧OC=弧CA,即C是劣弧OA的中点,如果连接O′C,根据垂径定理可得出O′C垂直平分OA,由此可求出C点的坐标;
(4)如果设O′C和OA的交点为E,可根据相似三角形OBD和ECD求出OD的长,那么如果S△ABD=S△POD,可据此求出三角形POD中OD边上的高,然后同圆O′中点到x轴的最大距离进行比较即可得出P是否在圆上.
解答:解:(1)连接AB.
∵∠BOA=90°,
∴AB是⊙的直径.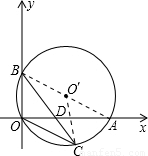
∴AB=13;
(2)∵OA2+OB2=AB2
即(OA+OB)2-2OA•OB=169
又∵OA、OB是方程x2+kx+60=0的两根
∴OA+OB=-k,OA•OB=60
∴k2-120=169.
∴k=17,k=-17.
∵OA+OB=-k>0,
∴k<0,
∴k=-17.
方程是x2-17x+60=0解出x=12,x=5.
∵OA>OB,
∴OA=12,OB=5;
(3)连接O′C,交AO于E
由OC2=CD•CB,得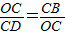 .
.
又∵∠OCB=∠DCO,
∴△OCB∽△DCO.
∴∠COD=∠CBO,
∴弧AC=弧OC,O′C⊥OA.
∴OE=AE=6,CE=O′C-O′E=O′C- OB=-4.
OB=-4.
∴C点坐标是(6,-4);
(4)假定在⊙上存在点P,使S△ABD=S△POD.
∵OB∥EC
∴△OBD∽△ECD
∴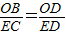 即
即 =
=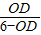
解得OD= .
.
∴S△ABD= AD•BO=
AD•BO=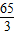 ,
,
∴S△POD=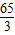
在中,OD边上的高为13,即点P到x轴的距离为13,
∵⊙上的点到x轴的最大距离为9,
∴点P不在⊙上,
故在⊙上不存在点P,使S△ABD=S△POD.
点评:本题考查了一元二次方程的根与系数的关系,二次函数解析式的确定、图形的面积求法、圆周角定理、相似三角形的判定和性质等知识及综合应用知识、解决问题的能力.
(2)可在直角三角形OBA中,根据勾股定理和韦达定理来求出OA,OB的长;
(3)已知了OC2=CD•BC,那么三角形OCD和BCO相似,因此∠OBC=∠DOC,此时可得出弧OC=弧CA,即C是劣弧OA的中点,如果连接O′C,根据垂径定理可得出O′C垂直平分OA,由此可求出C点的坐标;
(4)如果设O′C和OA的交点为E,可根据相似三角形OBD和ECD求出OD的长,那么如果S△ABD=S△POD,可据此求出三角形POD中OD边上的高,然后同圆O′中点到x轴的最大距离进行比较即可得出P是否在圆上.
解答:解:(1)连接AB.
∵∠BOA=90°,
∴AB是⊙的直径.

∴AB=13;
(2)∵OA2+OB2=AB2
即(OA+OB)2-2OA•OB=169
又∵OA、OB是方程x2+kx+60=0的两根
∴OA+OB=-k,OA•OB=60
∴k2-120=169.
∴k=17,k=-17.
∵OA+OB=-k>0,
∴k<0,
∴k=-17.
方程是x2-17x+60=0解出x=12,x=5.
∵OA>OB,
∴OA=12,OB=5;
(3)连接O′C,交AO于E
由OC2=CD•CB,得
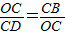 .
.又∵∠OCB=∠DCO,
∴△OCB∽△DCO.
∴∠COD=∠CBO,
∴弧AC=弧OC,O′C⊥OA.
∴OE=AE=6,CE=O′C-O′E=O′C-
 OB=-4.
OB=-4.∴C点坐标是(6,-4);
(4)假定在⊙上存在点P,使S△ABD=S△POD.
∵OB∥EC
∴△OBD∽△ECD
∴
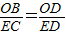 即
即 =
=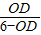
解得OD=
 .
.∴S△ABD=
 AD•BO=
AD•BO=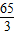 ,
,∴S△POD=
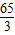
在中,OD边上的高为13,即点P到x轴的距离为13,
∵⊙上的点到x轴的最大距离为9,
∴点P不在⊙上,
故在⊙上不存在点P,使S△ABD=S△POD.
点评:本题考查了一元二次方程的根与系数的关系,二次函数解析式的确定、图形的面积求法、圆周角定理、相似三角形的判定和性质等知识及综合应用知识、解决问题的能力.

练习册系列答案
相关题目
 )
)