题目内容
已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y≤9,求这个一次函数解析式.
解:设该一次函数的关系式是:y=kx+b(k≠0).
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,相应函数值的取值范围是:5≤y≤9,则
①当k>0函数为递增函数,即x=2,y=5时,
x=6时,y=9.
根据题意列出方程组: ,
,
解得: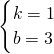 ,
,
则这个函数的解析式是:y=x+3;
②当k<0函数为递减函数时,
则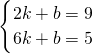 ,
,
解得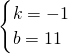 ,
,
所以该一次函数的解析式为y=-x+11,
综上所述,该一次函数的解析式是y=x+3,或y=-x+11.
分析:根据自变量的取值范围确定x,y的值,用待定系数法可求出函数关系式.
点评:本题考查了一次函数的性质、待定系数法求一次函数的解析式;解答该题时,采用了分类讨论的方法,以防漏解.
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,相应函数值的取值范围是:5≤y≤9,则
①当k>0函数为递增函数,即x=2,y=5时,
x=6时,y=9.
根据题意列出方程组:
 ,
,解得:
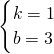 ,
,则这个函数的解析式是:y=x+3;
②当k<0函数为递减函数时,
则
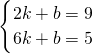 ,
,解得
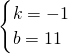 ,
,所以该一次函数的解析式为y=-x+11,
综上所述,该一次函数的解析式是y=x+3,或y=-x+11.
分析:根据自变量的取值范围确定x,y的值,用待定系数法可求出函数关系式.
点评:本题考查了一次函数的性质、待定系数法求一次函数的解析式;解答该题时,采用了分类讨论的方法,以防漏解.

练习册系列答案
相关题目
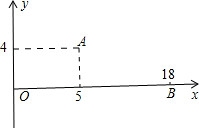 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.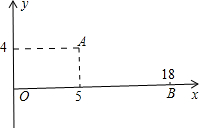 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
