题目内容
某商场为了吸引顾客,设立一个可自由转动的转盘,(如图3个数字所在的扇形面积相等)并规定,顾客每购满100元商品,可转动两次转盘,转盘停止后,看指针指向的数,(如果指针指向分界线,则重新转动转盘,直到指针指向数为止)获奖方法是:①指针两次都指向3,顾客可获得90元购物券,②指针只有一次指向3,顾客可获得36元购物券,③指针两次都不指向3,且两次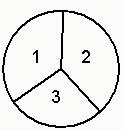 指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.
指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.(1)试用树形图或列表法给出两次转动转盘指针所有可能指向的结果;
(2)试求顾客获得90元购物券的概率;
(3)你认为转动转盘和直接获得购物券哪种方式更合算?试说明理由.
分析:(1)用列表法列举出所有情况,看所求的情况与总情况的比值即可得答案;
(2)由(1)的图表,根据题意分析可得顾客获得90元购物券的情况数目,作比可得答案;
(3)算出每转动两次转盘所获得购物券金额的平均数,与直接获得购物券比较可得答案.
(2)由(1)的图表,根据题意分析可得顾客获得90元购物券的情况数目,作比可得答案;
(3)算出每转动两次转盘所获得购物券金额的平均数,与直接获得购物券比较可得答案.
解答:解:(1)如下表:
(3分)
(2)P(获得90元)=
(6分)
(3)P(两次都指向3)=
,P(只有一次指向3)=
,
每转动两次转盘所获得购物券金额的平均数为:
×90+
×36+
×3×9+
×3×9=32>30,
所以转动转盘合算(10分).
| 第一次 第二次 |
1 | 2 | 3 |
| 1 | (1,1) | (2,1) | (3,1) |
| 2 | (1,2) | (2,2) | (3,2) |
| 3 | (1,3) | (2,3) | (3,3) |
(2)P(获得90元)=
| 1 |
| 9 |
(3)P(两次都指向3)=
| 1 |
| 9 |
| 4 |
| 9 |
每转动两次转盘所获得购物券金额的平均数为:
| 1 |
| 9 |
| 4 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |
所以转动转盘合算(10分).
点评:列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.易错点是得到每转动两次转盘所获得购物券金额的平均数.

练习册系列答案
相关题目
 21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.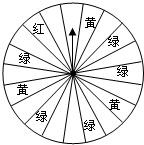 某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少?
某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少? 某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为
某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为