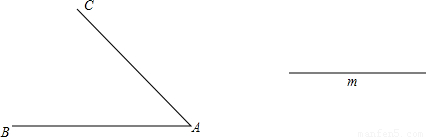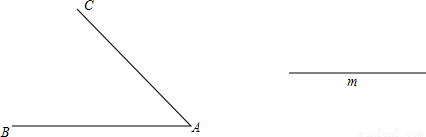题目内容
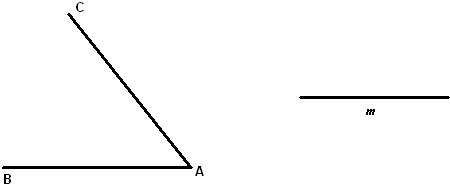
 有两条交叉公路AB和CD交于点C,在公路CD旁有甲、乙两个村庄(可近似看作甲、乙两个村庄在公路CD上),如图所示,两村准备合资在两条公路之间的空地上建一个食品加工厂,要求加工厂到两条公路和到两个村的距离都相等.
有两条交叉公路AB和CD交于点C,在公路CD旁有甲、乙两个村庄(可近似看作甲、乙两个村庄在公路CD上),如图所示,两村准备合资在两条公路之间的空地上建一个食品加工厂,要求加工厂到两条公路和到两个村的距离都相等.(1)在图中确定要建的食品加工厂的位置;(保留作图痕迹,不必写作法)
(2)建好食品加工厂以后,又修了一条食品加工厂通向甲村的公路,该公路恰好与公路AB平行,已知交叉口C与甲村之间的公路长2km,甲、乙两村相距2km,求食品加工厂到公路AB的距离.(保留根号)
分析:(1)利用角平分线的作法以及线段垂直平分线的作法作图即可;
(2)利用角平分线的性质以及线段垂直平分线的性质和勾股定理求出PF的长度即可.
(2)利用角平分线的性质以及线段垂直平分线的性质和勾股定理求出PF的长度即可.
解答: 解:(1)如图所示:点P即为所求;
解:(1)如图所示:点P即为所求;
(2)过点P作PF⊥AB于点F,
∵CP平分∠DCB,
∴∠DCP=∠PCB,
∵MP∥AB,
∴∠MPC=∠PCF,
∴∠MCP=∠MPC,
∴MC=MP=2,
∵PE垂直平分MO,
∴ME=EO=1,
∴PE=
=
(km),
∵PE⊥CE,PF⊥BC,∠ECP=∠PCB,
∴PE=PF=
(km).
答:食品加工厂到公路AB的距离为
km.
 解:(1)如图所示:点P即为所求;
解:(1)如图所示:点P即为所求;(2)过点P作PF⊥AB于点F,
∵CP平分∠DCB,
∴∠DCP=∠PCB,
∵MP∥AB,
∴∠MPC=∠PCF,
∴∠MCP=∠MPC,
∴MC=MP=2,
∵PE垂直平分MO,
∴ME=EO=1,
∴PE=
| 22-12 |
| 3 |
∵PE⊥CE,PF⊥BC,∠ECP=∠PCB,
∴PE=PF=
| 3 |
答:食品加工厂到公路AB的距离为
| 3 |
点评:此题主要考查了应用与设计作图,熟练根据角平分线的性质以及线段垂直平分线的性质得出PE=PF是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目