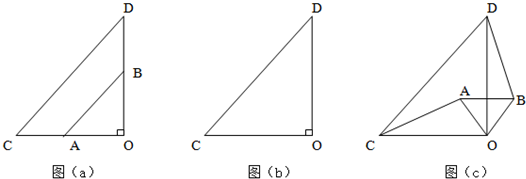
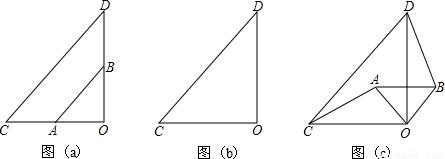
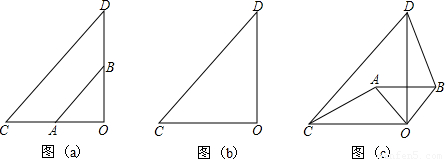
题目内容
如图(a),两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O。

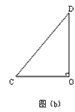
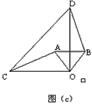
(1)将图(a)中的△OAB绕点O顺时针旋转90°角,在图(b)中作出旋转后的△OAB(保留作图痕迹,不写作法,不证明);
(2)在图(b)中,你发现线段AC、BD的数量关系是___,直线AC、BD相交成____度角;(说明理由)(3)将图(a)中的△OAB绕点O顺时针旋转一个锐角,得到图(c),这时(2)中的两个结论是否成立?作出判断并说明理由。若△OAB绕点O继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由。
(2)在图(b)中,你发现线段AC、BD的数量关系是___,直线AC、BD相交成____度角;(说明理由)(3)将图(a)中的△OAB绕点O顺时针旋转一个锐角,得到图(c),这时(2)中的两个结论是否成立?作出判断并说明理由。若△OAB绕点O继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由。
解:(1)如图:
 ;
;
(2)AC=BD,AC、BD相交成90 度;
(3)成立,理由是:延长CA交OD于E,交BD与F
在△ACO和△BDO中
AO=BO ,∠AOC=∠BOD ,OC=OD
△ACO≌△BDO(SAS)
∴AC=BD,∠OCA=∠ODB
∵∠OCA+∠OEC=90°
又∠OEC=∠DEF
∴∠ODB+∠DEF=90°
∴∠DFE=90°
∴AC、BD相交成90 度。
AC=BD,AC、BD相交成90 度。
 ;
;(2)AC=BD,AC、BD相交成90 度;
(3)成立,理由是:延长CA交OD于E,交BD与F
在△ACO和△BDO中
AO=BO ,∠AOC=∠BOD ,OC=OD
△ACO≌△BDO(SAS)
∴AC=BD,∠OCA=∠ODB
∵∠OCA+∠OEC=90°
又∠OEC=∠DEF
∴∠ODB+∠DEF=90°
∴∠DFE=90°
∴AC、BD相交成90 度。
AC=BD,AC、BD相交成90 度。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目