题目内容
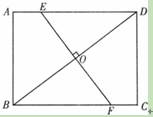
(2011•潍坊)已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
A、CP平分∠BCD B、四边形ABED为平行四边形
C、CQ将直角梯形分为面积相等的两部分 D、△ABF为等腰三角形
C解析:
证明:易证△BCF≌△DCE(SAS),
∴∠FBC=∠EDC,BF=ED;
∴△BPE≌△DPF(AAS),
∴BP=DP,
∴△BPC≌△DPC(SSS),
∴∠BCP=∠DCP,即A正确;
又∵AD=BE且AB∥BE,
∴四边形ABED为平行四边形,B正确;
∵BF=ED,AB=ED,
∴AB=BF,即D正确;
综上,选项A、B、D正确;故选C.
证明:易证△BCF≌△DCE(SAS),
∴∠FBC=∠EDC,BF=ED;
∴△BPE≌△DPF(AAS),
∴BP=DP,
∴△BPC≌△DPC(SSS),
∴∠BCP=∠DCP,即A正确;
又∵AD=BE且AB∥BE,
∴四边形ABED为平行四边形,B正确;
∵BF=ED,AB=ED,
∴AB=BF,即D正确;
综上,选项A、B、D正确;故选C.

练习册系列答案
相关题目