题目内容
抛掷红、蓝两枚六面编号分别为1~6(整数)的质地均匀的正方体骰子,将红色和蓝色骰子正面朝上的编号分别作为二次函数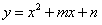 的一次项系数m和常数项n的值。
的一次项系数m和常数项n的值。
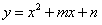 的一次项系数m和常数项n的值。
的一次项系数m和常数项n的值。 (1)问这样可以得到多少个不同形式的二次函数?(只需写出结果)
(2)请求出抛掷红、蓝骰子各一次,得到的二次函数图象顶点恰好在轴上的概率是多少?并说明理由。
(2)请求出抛掷红、蓝骰子各一次,得到的二次函数图象顶点恰好在轴上的概率是多少?并说明理由。
解:(1)可以得到36个不同形式的二次函数。
(2) ,
,
∵二次函数图象顶点在 轴上,
轴上,
∴ ,即
,即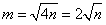 (其中n,m为1~6的整数),
(其中n,m为1~6的整数),
根据上式可知,当n取1~6中的完全平方数时上式才可能成立。
∴n的值只能取完全平方数1和4,
通过计算可知,当 和
和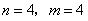 满足
满足 。
。
由此抛掷红、蓝骰子各一次,得到的二次函数图象顶点在 轴上的概率是
轴上的概率是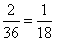 。
。
(2)
 ,
,∵二次函数图象顶点在
 轴上,
轴上,∴
 ,即
,即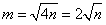 (其中n,m为1~6的整数),
(其中n,m为1~6的整数),根据上式可知,当n取1~6中的完全平方数时上式才可能成立。
∴n的值只能取完全平方数1和4,
通过计算可知,当
 和
和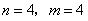 满足
满足 。
。由此抛掷红、蓝骰子各一次,得到的二次函数图象顶点在
 轴上的概率是
轴上的概率是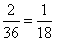 。
。
练习册系列答案
相关题目