题目内容
如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB'C'的位置.若∠CAB'=25°则∠ACC''的度数为（ ）
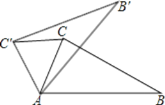
A. 25° B. 40° C. 65° D. 70°
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB'C'的位置.若∠CAB'=25°则∠ACC''的度数为（ ）
A. 25° B. 40° C. 65° D. 70°
天天向上一本好卷系列答案小学生10分钟应用题系列答案
= __________．
有意义，则x的取值范围是________．