题目内容
观察下列算式,你会发现什么规律?
1×3+1=4=22:
2×4+1=9=32:
3×5+1=16=42:
4×6+1=25=52
…
请你把发现的规律用含字母n(n≥2且n为整数)的式子表示出来.
1×3+1=4=22:
2×4+1=9=32:
3×5+1=16=42:
4×6+1=25=52
…
请你把发现的规律用含字母n(n≥2且n为整数)的式子表示出来.
分析:根据已知式子中数据得出数据之间的变化,第一个数比第二个数小2,它们的乘积等于这两个数之间的数的平方,进而得出答案.
解答:解:∵1×3+1=4=22:
2×4+1=9=32:
3×5+1=16=42:
4×6+1=25=52
…
∴(n-1)(n+1)+1=n2(n≥2)
2×4+1=9=32:
3×5+1=16=42:
4×6+1=25=52
…
∴(n-1)(n+1)+1=n2(n≥2)
点评:此题主要考查了数字变化规律,根据已知数据得出数据的变与不变是解题关键.

练习册系列答案
相关题目
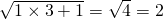 ;
;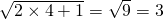 ;
;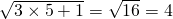 ;
;