题目内容
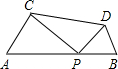如图，已知AB=10，P是线段AB上任意一点，在AB的同侧分别以AP和PB为边作两个等边三角形APC和BPD，则线段CD的长度的最小值是（ ）| A、4 | ||
| B、5 | ||
| C、6 | ||
D、5(
|
分析：过C作CE⊥AB于E，过D作DF⊥PB于F，过D作DG⊥CE于G，根据勾股定理可以求得CD=
，根据CG的取值范围可以求得CD的最小值，即可解题．
| EF2+CG2 |
解答：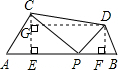
解：如图过C作CE⊥AB于E，过D作DF⊥PB于F，过D作DG⊥CE于G．
显然DG=EF=
AB=5，CD≥DG，
∴CD=
，故CG=0时，CD有最小值，
当P为AB中点时，有CD=DG=5，
所以CD长度的最小值是5．
故选B．
解：如图过C作CE⊥AB于E，过D作DF⊥PB于F，过D作DG⊥CE于G．显然DG=EF=
| 1 |
| 2 |
∴CD=
| EF2+CG2 |
当P为AB中点时，有CD=DG=5，
所以CD长度的最小值是5．
故选B．
点评：本题考查了勾股定理在直角三角形中的灵活运用，等边三角形各边长相等的性质，本题中根据勾股定理计算CD的值是解题的关键．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
23、如图：已知AB=10，点C、D在线段AB上且AC=DB=2；P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是
（2013•郴州模拟）如图，已知AB=10，C是线段AB上一动点，分别以AC、BC为斜边作直角△ACD、直角△BCE，且∠A=60°，∠B=30°，连接DE，M是DE的中点．
如图，已知AB=10，P是线段AB上的动点，分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB，连接CD，设CD的中点为G，当点P从点A运动到点B时，则点G移动路径的长是
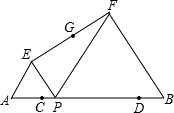如图：已知AB=10，点C、D在线段AB上且AC=DB=2； P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是（ ）
如图，已知AB=10，点C为AB上一点，且AC：CB=3：2，DE分别为AC，AB的中点，则DE的长是