题目内容
描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为 ],现有甲、乙两个样本,
],现有甲、乙两个样本,
甲:13,11,15,10,16;
乙:11,16,6,13,19
(1)分别计算甲、乙两个样本的“平均差”,并根据计算结果判断哪个样本波动较大.
(2)分别计算甲、乙两个样本的“方差”,并根据计算结果判断哪个样本波动较大.
(3)以上的两种方法判断的结果是否一致?
解:(1)甲组的平均数为(13+11+15+10+16)÷=13,
T甲=(0+2+2+3+3)÷5=2,
乙组的平均数为(11+16+6+13+19)÷5=13,
T乙=(2+3+7+0+6)÷5=3.6.
3.6>2,
则乙样本波动较大.
(2)甲的方差= [(13-13)2+(11-13)2+(15-13)2+(10-13)2+(16-13)2]=5.2.
[(13-13)2+(11-13)2+(15-13)2+(10-13)2+(16-13)2]=5.2.
乙的方差= [(11-13)2+(16-13)2+(6-13)2+(13-13)2+(19-13)2]=19.6.
[(11-13)2+(16-13)2+(6-13)2+(13-13)2+(19-13)2]=19.6.
∵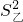 <
<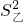 ,
,
∴乙样本波动较大;
(3)通过(1)和(2)的计算,结果一致.
分析:(1)由平均数的公式计算出甲和乙的平均数,再根据平均差公式进行计算即可;
(2)根据方差公式进行计算,再根据方差越大,波动性越大,即可得出答案;
(3)通过(1)和(2)得出的数据,即可得出两种方法判断的结果一样.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2=
,则方差S2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
T甲=(0+2+2+3+3)÷5=2,
乙组的平均数为(11+16+6+13+19)÷5=13,
T乙=(2+3+7+0+6)÷5=3.6.
3.6>2,
则乙样本波动较大.
(2)甲的方差=
 [(13-13)2+(11-13)2+(15-13)2+(10-13)2+(16-13)2]=5.2.
[(13-13)2+(11-13)2+(15-13)2+(10-13)2+(16-13)2]=5.2.乙的方差=
 [(11-13)2+(16-13)2+(6-13)2+(13-13)2+(19-13)2]=19.6.
[(11-13)2+(16-13)2+(6-13)2+(13-13)2+(19-13)2]=19.6.∵
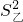 <
<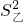 ,
,∴乙样本波动较大;
(3)通过(1)和(2)的计算,结果一致.
分析:(1)由平均数的公式计算出甲和乙的平均数,再根据平均差公式进行计算即可;
(2)根据方差公式进行计算,再根据方差越大,波动性越大,即可得出答案;
(3)通过(1)和(2)得出的数据,即可得出两种方法判断的结果一样.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
 ,则方差S2=
,则方差S2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 
练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
在一组数据x1,x2,…,xn中,各数据与它们的平均数
的差的绝对值的平均数,即T=
(|x1-
|+|x2-
|+…|xn-
|)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度.“平均差”越大说明数据的离散程度越大.因为“平均差”的计算要比方差的计算要容易一点,所以有时人们也用它来代替方差来比较数据的离散程度.极差、方差(标准差)、平均差都是反映数据离散程度的量.
一水产养殖户李大爷要了解鱼塘中鱼的重量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况;为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度几个的量中某些值超标时就要捕捞;分开养殖或出售;他从两个鱼塘各随机捕捞10条鱼称得重量如下:(单位:千克)
A鱼塘:3、5、5、5、7、7、5、5、5、3
B鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算甲、乙两个鱼塘中抽取的样本的极差、方差、平均差;完成下面的表格:
(2)如果你是技术人员,你会建议李大爷注意哪个鱼塘的风险更大些?计算哪些量更能说明鱼重量的离散程度?
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
一水产养殖户李大爷要了解鱼塘中鱼的重量的离散程度,因为个头大小差异太大会出现“大鱼吃小鱼”的情况;为防止出现“大鱼吃小鱼”的情况,在能反映数据离散程度几个的量中某些值超标时就要捕捞;分开养殖或出售;他从两个鱼塘各随机捕捞10条鱼称得重量如下:(单位:千克)
A鱼塘:3、5、5、5、7、7、5、5、5、3
B鱼塘:4、4、5、6、6、5、6、6、4、4
(1)分别计算甲、乙两个鱼塘中抽取的样本的极差、方差、平均差;完成下面的表格:
| 极差 | 方差 | 平均差 | |
| A鱼塘 | |||
| B鱼塘 |