题目内容
将边长分别为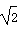 ,2
,2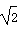 ,3
,3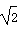 ,
,
4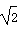 …的正方形的面积记作S1,S2,S3,
…的正方形的面积记作S1,S2,S3,
S4…,计算S2- S1,S3-S2,S4-S3…,若
边长为n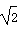 (n为正整数)的正方形面积
(n为正整数)的正方形面积
记作Sn,根据你计算的规律,猜想:
Sn+1-Sn=
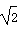 ,2
,2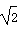 ,3
,3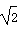 ,
,4
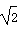 …的正方形的面积记作S1,S2,S3,
…的正方形的面积记作S1,S2,S3,S4…,计算S2- S1,S3-S2,S4-S3…,若
边长为n
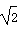 (n为正整数)的正方形面积
(n为正整数)的正方形面积记作Sn,根据你计算的规律,猜想:
Sn+1-Sn=
4n+2
根据题意计算出所给边长对应的正方形的面积,根据面积差得出规律:S2-S1=6,S3-S2=10,S4-S3=14,总结出规律即可得出答案.
解:∵S1=2,S2=8,S3=18,S4=32,
∴S2-S1=6,S3-S2=10,S4-S3=14,
据上可得出Sn+1-Sn=2(n+1+n)=4n+2,
故答案为:4n+2.
解:∵S1=2,S2=8,S3=18,S4=32,
∴S2-S1=6,S3-S2=10,S4-S3=14,
据上可得出Sn+1-Sn=2(n+1+n)=4n+2,
故答案为:4n+2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ▲ .
▲ .
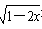 有意义,则x的取值范围是_ ▲ .
有意义,则x的取值范围是_ ▲ .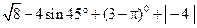
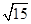 最接近的数是( )
最接近的数是( ) 、
、 为实数,且
为实数,且 ,则
,则 = ▲ .
= ▲ .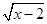 +
+ = 0,则
= 0,则 的值为
的值为


