题目内容
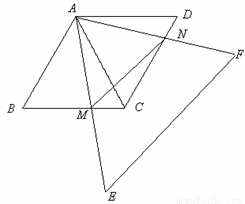
(本题7分)如图,等腰直角△ABC中,∠ABC=90°,点D在AC上, 将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.

⑴求∠DCE的度数;
⑵当AB=4,AD:DC=1: 3时,求DE的长.
解:(1)∵△CBE是由△ABD旋转得到的,∴△ABD≌△CBE,…………1分
∴∠A=∠BCE=45°,……………………………………………………………2分
∴∠DCE=∠DCB+∠BCE=90° ………………………………………………3分
(2)∵在等腰直角三角形ABC中,∵AB=4,∴AC=4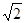 ……………………4分
……………………4分
又∵AD︰DC=1︰3,∴AD=![]() ,DC=3
,DC=3![]() ,…………………………………………5分
,…………………………………………5分
由(1)知AD=CE且∠DCE=90°, ………………………………………………6分
∴DE![]() =DC
=DC![]() +CE
+CE![]() =2+18=20,∴DE=2
=2+18=20,∴DE=2![]() …………………………………7分
…………………………………7分
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )cm,正六边形的边长为(
)cm,正六边形的边长为(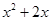 )cm
)cm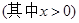 .求这两段铁丝的总长
.求这两段铁丝的总长
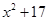 )cm,正六边形的边长为(
)cm,正六边形的边长为(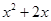 )cm
)cm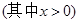 .求这两段铁丝的总长
.求这两段铁丝的总长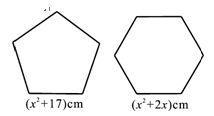

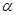 ,△BOC ≌△ADC,∠OCD=60°,连接OD。
,△BOC ≌△ADC,∠OCD=60°,连接OD。