题目内容
若函数y=(a+3b)x+(2-a)是正比例函数且图象经过第二、四象限,试化简:|1-b|+
.
| 9b2+12b+4 |
分析:先根据正比例函数的定义及其图象的性质,可得a=2及b的取值范围,再根据绝对值的定义、二次根式的性质化简即可.
解答:解:∵函数y=(a+3b)x+(2-a)是正比例函数且图象经过第二、四象限,
∴2-a=0,a+3b<0,
∴a=2,3b+2<0,
∴b<-
,
∴|1-b|+
=1-b-(3b+2)=-1-4b.
∴2-a=0,a+3b<0,
∴a=2,3b+2<0,
∴b<-
| 2 |
| 3 |
∴|1-b|+
| 9b2+12b+4 |
点评:本题考查了正比例函数的定义及其图象的性质,绝对值的定义、二次根式的性质与化简,难度适中,是基础知识,需牢固掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
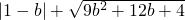 .
.