题目内容
用三块正多边形的木块铺地,拼在一起相交于一点的各边完全吻合,设它们的边数为m、n、p,则
- A.

- B.

- C.

- D.
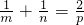
B
分析:正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.本题根据位于同一顶点处的三个角之和为360°,由n边形的内角和公式及正n边形的性质,列出方程,将方程变形即可求解.
解答:∵n边形的内角和为180°×(n-2),正n边形的每一个内角相等,
∴正n边形的内角为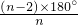 .
.
∵用三块正多边形的木块铺地,拼在一起相交于一点的各边完全吻合,
∴位于同一顶点处的三个角之和为360°.
又∵这三块正多边形的边数为m、n、p,
∴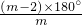 +
+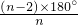 +
+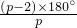 =360°,
=360°,
∴(180-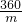 )+(180-
)+(180- )+(180-
)+(180-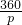 )=360,
)=360,
∴ +
+ +
+ =
= .
.
故选B.
点评:解决此类题,可以记住几个常用正多边形的内角,及能够用三种正多边形镶嵌的组合.
分析:正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.本题根据位于同一顶点处的三个角之和为360°,由n边形的内角和公式及正n边形的性质,列出方程,将方程变形即可求解.
解答:∵n边形的内角和为180°×(n-2),正n边形的每一个内角相等,
∴正n边形的内角为
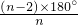 .
.∵用三块正多边形的木块铺地,拼在一起相交于一点的各边完全吻合,
∴位于同一顶点处的三个角之和为360°.
又∵这三块正多边形的边数为m、n、p,
∴
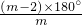 +
+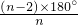 +
+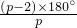 =360°,
=360°,∴(180-
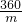 )+(180-
)+(180- )+(180-
)+(180-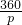 )=360,
)=360,∴
 +
+ +
+ =
= .
.故选B.
点评:解决此类题,可以记住几个常用正多边形的内角,及能够用三种正多边形镶嵌的组合.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
用三块正多边形的木块铺地,拼在一起相交于一点的各边完全吻合,设它们的边数为m、n、p,则( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|



