题目内容
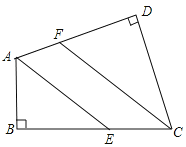
【题目】已知：如图，四边形ABCD中，AD⊥DC，BC⊥AB，AE平分∠BAD，CF平分∠DCB，AE交CD于E，CF交AB于F，问AE与CF是否平行？为什么？
【答案】见解析
【解析】想证明AE与CF平行需构造应用平行线判定方法的条件，∠DEA和∠DCF是直线AE与FC被直线CD所截而成的同位角，根据垂直的定义和角平分线的性质可结合图形证得∠DEA=∠DCF，再根据同位角相等，两直线平行可得AE∥CF．
解：平行．理由如下：
∵AD⊥DC，BC⊥AB，
∴∠D=∠B=90°．
∵∠DAB+∠B+∠BCD+∠D=360°，
∴∠DAB+∠BCD=180°．
∵AE平分∠BAD，CF平分∠DCB，
∴∠DAE+∠DCF=90°．
∵∠D+∠DFC+∠DCF=180°，
∴∠DFC+∠DCF=90°．
∴∠DAE=∠DFC
∴AE∥CF．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
