题目内容
在△ABC中,三边之比为a:b:c=1:
:2.则sinA+tanA等于( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先根据三角形三边之比判断出三角形的形状,再根据直角三角形的性质求出∠A的度数,运用特殊角的三角函数值求解.
解答:解:∵△ABC中,三边之比为a:b:c=1:
:2,
∴a2+b2=1+3=4=c2,△ABC是直角三角形,且c为斜边.
∵a=
c,∴
=
=sinA,
∴∠A=30°.
sinA+tanA=sin30°+tan30°=
+
=
.
故选A.
| 3 |
∴a2+b2=1+3=4=c2,△ABC是直角三角形,且c为斜边.
∵a=
| 1 |
| 2 |
| a |
| c |
| 1 |
| 2 |
∴∠A=30°.
sinA+tanA=sin30°+tan30°=
| 1 |
| 2 |
| ||
| 3 |
3+2
| ||
| 6 |
故选A.
点评:本题考查了勾股定理的逆定理及特殊角的三角函数值,是中学阶段的重点.

练习册系列答案
相关题目
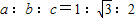 ,则sinA+cosA=
,则sinA+cosA=  ,则sinA+cosA=
,则sinA+cosA=