题目内容
【题目】某旅行社带一旅游团来宜春明月山游玩，晚上入住温汤某酒店，现需要订9个房间，酒店房间分为两种：A种房间200元/间，B种房间160/间，在费用不超过1700元的情况下，要求A种房间的数量不少于B种房间数量的一半．若设订A种房间x间，请你解答下列问题：
（1）共有几种符合题意的订房方案？写出解答过程．
（2）根据计算判断：哪种订房方案更省钱？
【答案】
（1）解：设A种房间的数量为x，则B种房间的数量为（9﹣x）．
依题意可得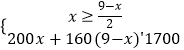 
，
解得：3≤x≤ 
．
∵x为整数，
∴x=3或x=4或x=5或x=6．
∴共有4种方案：①3间A，6间B；②4间A，5间B；③5间A，4间B；④6间A，3间B
（2）解：∵当A种房间越少，所需费用最低，
∴当x=3时，时，最低费用为3×200+6×160=1560元
【解析】（1）设A种房间的数量为x，则B种房间的数量为（9﹣x），然后依据A种房间的数量不少于B种房间数量的一半；总费用不超过1700元列不等式组可求得x的范围，然后由x为正整数，从而可确定出所有的方案；（2）由于A种房间的单间较高，故此x越小费用越低，从而可得到当x=3时，总费用最低，然后求得最低费用即可．
【考点精析】通过灵活运用一元一次不等式组的应用，掌握1、审：分析题意，找出不等关系；2、设：设未知数；3、列：列出不等式组；4、解：解不等式组；5、检验：从不等式组的解集中找出符合题意的答案；6、答：写出问题答案即可以解答此题．
练习册系列答案
相关题目
