题目内容
（2004•苏州）如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=（ ）
A．15°
B．20°
C．30°
D．45°
【答案】分析：连接OC，BC，根据弦CD垂直平分OB，得OC=BC，又OC=OB，所以△OCB是等边三角形，得∠COB=60°，根据圆周角定理得∠D=30°．
解答：
解：连接OC，BC
∵弦CD垂直平分OB
∴OC=BC
∵OC=OB
∴△OCB是等边三角形
∴∠COB=60°
∴∠D=30°．
故选C．
点评：此题要根据线段垂直平分线的性质证出等边三角形，再熟练运用圆周角定理求解．
解答：
解：连接OC，BC∵弦CD垂直平分OB
∴OC=BC
∵OC=OB
∴△OCB是等边三角形
∴∠COB=60°
∴∠D=30°．
故选C．
点评：此题要根据线段垂直平分线的性质证出等边三角形，再熟练运用圆周角定理求解．
练习册系列答案
发散思维新课堂系列答案
相关题目
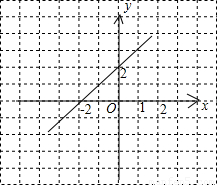
，则该矩形的两条对角线所成的锐角是（ ）
