题目内容
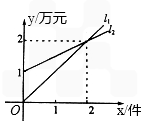
如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与 机床销售量的关系
机床销售量的关系(1)求l1、l2对应的函数表达式;
(2)当销售量为1件时,销售收入、销售成本、销售利润各是多少?
(3)请你写出利润与销售量之间的函数表达式;
(4)要使该公司赢利,你对该公司有何建议?
分析:(1)根据图象所过特殊点,用待定系数法求函数表达式;
(2)当x=1时,分别计算收入和成本,求利润;
(3)利润=收入-成本;
(4)根据利润表达式,运用函数的性质,结合实际提出建议.
(2)当x=1时,分别计算收入和成本,求利润;
(3)利润=收入-成本;
(4)根据利润表达式,运用函数的性质,结合实际提出建议.
解答:解:(1)设l1对应的函数表达式是 y=ax.
因为l1经过点(2,2),
则2a=2,
∴a=1.
故l1对应的函数表达式是y=x;
设l2对应的函数表达式是 y=kx+b.
因为l2经过点(0,1)、(2,2),
则
,
解得
.
故l2对应的函数表达式y=
x+1;
(2)当销售量为1件时,即x=1时,
销售收入是1万元;销售成本是1.5万元,
故销售利润是 1-1.5=-0.5万元;
(3)利润与销售量之间的函数表达式y=x×1-(
x+1)×1,即y=
x-1;
(4)建议增加销售量,每天至少销售3件.y=x×1-(
x+1)×1
因为l1经过点(2,2),
则2a=2,
∴a=1.
故l1对应的函数表达式是y=x;
设l2对应的函数表达式是 y=kx+b.
因为l2经过点(0,1)、(2,2),
则
|
解得
|
故l2对应的函数表达式y=
| 1 |
| 2 |
(2)当销售量为1件时,即x=1时,
销售收入是1万元;销售成本是1.5万元,
故销售利润是 1-1.5=-0.5万元;
(3)利润与销售量之间的函数表达式y=x×1-(
| 1 |
| 2 |
| 1 |
| 2 |
(4)建议增加销售量,每天至少销售3件.y=x×1-(
| 1 |
| 2 |
点评:此题考查一次函数的应用,用待定系数法求函数关系式是基础,理顺成本、收入、利润之间的关系是应用的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
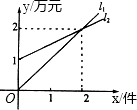 机床销售量的关系
机床销售量的关系