题目内容
【题目】如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD. 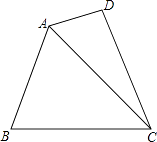
(1)求∠ADC的度数;
(2)若AB=10cm,CD=12cm,求四边形ABCD的面积.
【答案】
(1)解:作CE⊥AB交AB于点E,则∠AEC=90°,
∵AC=BC,
∴CE是AB的垂直平分线,
∴AE=BE= ![]() AB,
AB,
∵AB=2AD,
∴AE=AD= ![]() AB,
AB,
∵∠AC平分∠BAD,
∴∠EAC=∠DAC,
在△ADC和△AEC中,
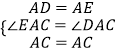 ,
,
∴△ADC≌△AEC,
∴∠ADC=∠AEC=90°
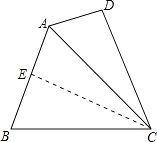
(2)解:∵CE是AB的垂直平分线,
∴S△ACD=S△AEC,
∵AB=2AD,CD=CE,
∴S△ACB=2S△ADC,
∴四边形ABCD的面积=3S△ADC=3× ![]() ×5×12=90cm2.
×5×12=90cm2.
【解析】(1)作CE⊥AB交AB于点E,则∠AEC=90°,利用已知条件和全等三角形的判定方法可证明△ADC≌△AEC,利用全等三角形的性质即可得到∠ADC=∠AEC=90°;(2)由(1)可知S△ACD=S△AEC , 再根据高相等的两个三角形面积比等于底之比可得S△ACB=2S△ADC , 进而四边形ABCD的面积=3S△ADC , 问题得解.

练习册系列答案
相关题目