题目内容
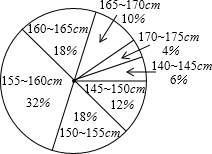
我市某校为了了解八年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm).

根据提供的信息,解答下列问题:
(1)求本次抽样调查的学生人数,并补全频数分别直方图.
(2)该样本的中位数在统计图的哪个范围内?
(3)在统计图1中,求“身高在145~150cm部分”的扇形所对应的圆心角的度数.
(4)如果该样本的平均数为159cm,方差为0.8;该校九年级学生身高的平均数为159cm,方差为0.6,那么________(填“八年级”或“九年级”)学生的身高比较整齐.
解:(1)总数为:32÷32%=100,则160-165的频数为:100-6-12-18-32-10-4=18或100×18%=18.
根据数据正确补全频数分布直方图,如下图:
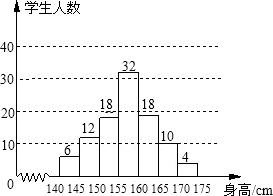
(2)第50和51个数的平均数在155~160cm的范围内,所以样本的中位数在155~160cm的范围内;
(3)12÷100×100%=12%;
(4)方差越小,数据的离散程度越小,所以九年级学生的身高比较整齐.
分析:(1)根据155-160的频数和百分比求总数.从而求出160-165的频数,根据数据正确补全频数分布直方图即可;
(2)根据中位数的确定方法求解;
(3)用身高在145-150的频数除以总数乘以周角的度数即可求得圆心角的度数.
(4)利用方差的意义判断.
点评:本题考查的是条形统计图和扇形统计图的综合运用;考查了中位数和方差的意义.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
根据数据正确补全频数分布直方图,如下图:


(2)第50和51个数的平均数在155~160cm的范围内,所以样本的中位数在155~160cm的范围内;
(3)12÷100×100%=12%;
(4)方差越小,数据的离散程度越小,所以九年级学生的身高比较整齐.
分析:(1)根据155-160的频数和百分比求总数.从而求出160-165的频数,根据数据正确补全频数分布直方图即可;
(2)根据中位数的确定方法求解;
(3)用身高在145-150的频数除以总数乘以周角的度数即可求得圆心角的度数.
(4)利用方差的意义判断.
点评:本题考查的是条形统计图和扇形统计图的综合运用;考查了中位数和方差的意义.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
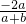 可变形为
可变形为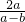
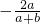
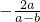
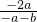
 如图,是一个几何体的主视图、左视图和俯视图,则这个几何体是
如图,是一个几何体的主视图、左视图和俯视图,则这个几何体是
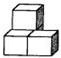
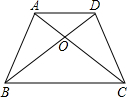 如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,
如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,