题目内容
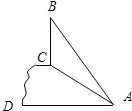如图，斜坡AC的坡度（坡比）为1：| 3 |
分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．
解答：
解：延长BC交AD于E点，则CE⊥AD．
在Rt△AEC中，AC=10，由坡比为1：
可知：∠CAE=30°，
∴CE=AC•sin30°=10×
=5，
AE=AC•cos30°=10×
=5
．
在Rt△ABE中，BE=
=
=11．
∵BE=BC+CE，∴BC=BE-CE=11-5=6（米）．
答：旗杆的高度为6米．
解：延长BC交AD于E点，则CE⊥AD．在Rt△AEC中，AC=10，由坡比为1：
| 3 |
∴CE=AC•sin30°=10×
| 1 |
| 2 |
AE=AC•cos30°=10×
| ||
| 2 |
| 3 |
在Rt△ABE中，BE=
| AB2-AE2 |
142-(5
|
∵BE=BC+CE，∴BC=BE-CE=11-5=6（米）．
答：旗杆的高度为6米．
点评：两个直角三角形有公共的直角边，先求出公共边的解决此类题目的基本出发点．
练习册系列答案
相关题目
，AC＝10米．坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度． 
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．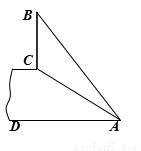 
，AC＝10米．坡顶有