题目内容
（2001•青海）在△ABC中，已知∠A=74°37′，∠B=60°23′，那么∠C= 度；sinC+cosC= ．
【答案】分析：根据三角形的内角和定理求∠C；运用特殊角的三角函数值计算．
解答：解：∠C=180°-74°37′-60°23’=45°，
sinC+cosC=sin45°+cos45°=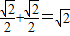
．
点评：此题主要考查三角形的内角和定理和特殊角的三角函数值．
解答：解：∠C=180°-74°37′-60°23’=45°，
sinC+cosC=sin45°+cos45°=
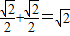．点评：此题主要考查三角形的内角和定理和特殊角的三角函数值．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
米，旗杆AB高为3米，C点的垂直高度为3.5米，C点与O点的水平距离为7米，以O为坐标原点，水平方向与竖直方向分别为x轴、y轴，建立直角坐标系．
米，旗杆AB高为3米，C点的垂直高度为3.5米，C点与O点的水平距离为7米，以O为坐标原点，水平方向与竖直方向分别为x轴、y轴，建立直角坐标系．
