题目内容
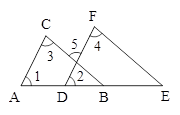
在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF
- A.同位角相等,两直线平行),
∴∠3=∠5 - B.内错角相等,两直线平行).
又∵∠3=∠4(已知)
∴∠5=∠4 - C.等量代换),
∴BC∥EF - D.内错角相等,两直线平行).
B
试题分析:根据平行线的判定和性质依次分析即可作出判断.
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.两直线平行,内错角相等).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
故选B.
考点:平行线的判定和性质
点评:本题属于基础应用题,只需学生熟练掌握平行线的判定和性质,即可完成.
试题分析:根据平行线的判定和性质依次分析即可作出判断.
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.两直线平行,内错角相等).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
故选B.
考点:平行线的判定和性质
点评:本题属于基础应用题,只需学生熟练掌握平行线的判定和性质,即可完成.

练习册系列答案
相关题目
在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF
| A.同位角相等,两直线平行), ∴∠3=∠5 | B.内错角相等,两直线平行). 又∵∠3=∠4(已知) ∴∠5=∠4 | C.等量代换), ∴BC∥EF | D.内错角相等,两直线平行). |


