��Ŀ����
����Ŀ����ͼ��������y=�� ![]() x2+bx+c��x�ύ�ڵ�A����B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
x2+bx+c��x�ύ�ڵ�A����B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��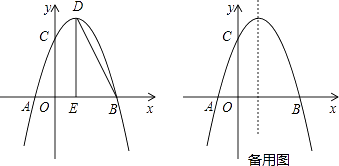
��1���������ߵĽ���ʽ����D�����ꣻ
��2����F���������ϵĶ��㣬����FBA=��BDEʱ�����F�����ꣻ
��3������M���������ϵĶ��㣬����M��MN��x���������߽��ڵ�N����P��x���ϣ���Q��ƽ���ڣ����߶�MNΪ�Խ�����������MPNQ����ֱ��д����Q�����꣮
���𰸡�
��1��
�⣺����B��6��0����C��0��6������y=�� ![]() x2+bx+c�У�
x2+bx+c�У�
�ã� ![]() ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+2x+6��
x2+2x+6��
��y=�� ![]() x2+2x+6=��
x2+2x+6=�� ![]() ��x��2��2+8��
��x��2��2+8��
���D��������2��8����
��2��
�⣺���߶�BF��y�ύ��Ϊ��F�䣬���F�������Ϊ��0��m������ͼ1��ʾ��
�ߡ�F��BO=��FBA=��BDE����F��OB=��BED=90�㣬
���F��BO�ס�BDE��
�� ![]() ��
��
�ߵ�B��6��0������D��2��8����
���E��2��0����BE=6��4=4��DE=8��0=8��OB=6��
��OF��= ![]() OB=3��
OB=3��
���F�䣨0��3����0����3����
��ֱ��BF�Ľ���ʽΪy=kx��3��
����0=6k+3��0=6k��3��
��ã�k=�� ![]() ��k=
��k= ![]() ��
��
��ֱ��BF�Ľ���ʽΪy=�� ![]() x+3��y=
x+3��y= ![]() x��3��
x��3��
����ֱ��BF�������ߵĽ���ʽ�ã�  �ٻ�
�ٻ�  �ڣ�
�ڣ�
�ⷽ����ٵã�  ��
�� ![]() ����ȥ����
����ȥ����
���F����������1�� ![]() ����
����
�ⷽ����ڵã�  ��
�� ![]() ����ȥ����
����ȥ����
���F����������3���� ![]() ����
����
���Ͽ�֪����F������Ϊ����1�� ![]() ����3����
����3���� ![]() ��
��

��3��
�⣺��Խ���MN��PQ���ڵ�O�䣬��ͼ2��ʾ��
�ߵ�M��N���������߶Գ���Գƣ����ı���MPNQΪ�����Σ�
���PΪ�����߶Գ�����x��Ľ��㣬��Q�������߶Գ����ϣ�
���Q��������2��2n�������M��������2��n��n����
�ߵ�M��������y=�� ![]() x2+2x+6��ͼ���ϣ�
x2+2x+6��ͼ���ϣ�
��n=�� ![]() +2��2��n��+6����n2+2n��16=0��
+2��2��n��+6����n2+2n��16=0��
��ã�n1= ![]() ��1��n2=��
��1��n2=�� ![]() ��1��
��1��
���Q��������2��2 ![]() ��2����2����2
��2����2����2 ![]() ��2����
��2����

����������1���ɵ�B��C���������ô���ϵ����������������ߵĽ���ʽ���������䷽���������߽���ʽ���γɶ���ʽ���ɵó����ۣ���2�����߶�BF��y�ύ��Ϊ��F�䣬���F�������Ϊ��0��m���������������ε��ж������ʿɵó���F������꣬���ݵ�B��F����������ô���ϵ���������ֱ��BF�Ľ���ʽ������ֱ��BF�������ߵĽ���ʽ�ɷ����飬�ⷽ���鼴�������F�����ꣻ��3����Խ���MN��PQ���ڵ�O�䣬��ͼ2��ʾ�����������ߵĶԳ��Խ�������ε����ʿɵó���P��Q��λ�ã������Q������Ϊ��2��2n�����������ε����ʿɵó���M������Ϊ��2��n��n�����ɵ�M��������ͼ���ϣ����ɵó�����n��һԪ���η��̣��ⷽ�̿����nֵ�������Q�����꼴�ɵó����ۣ����⿼���˴���ϵ������������ʽ�����������ε��ж������ʡ������ε����ʼ���һԪ���η��̣�����Ĺؼ��ǣ���1�����ô���ϵ���������������ʽ����2�����ֱ��BF�Ľ���ʽ����3���ó�����n��һԪ���η��̣����������е��⣬�ѶȲ������������Ŀʱ���ҳ�����������ô���ϵ���������������ʽ�ǹؼ���
�����㾫����������Ĺؼ��������������ε����ʵ����֪ʶ�������������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ��Լ������������ε����ʵ����⣬�˽��Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�