题目内容
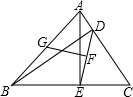
如图，已知AE，BD分别是三角形ABC的BC，AC边上的高，F是DE的中点，G是AB的中点，试说明GF与DE的位置关系．分析：如图，连接GE、GD构造等腰△DGE．利用等腰三角形“三合一”的性质证得GF⊥DE．
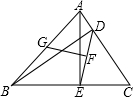
解答：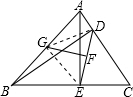
解：GF⊥DE．理由如下：
如图，连接GE、GD．
∵AE，BD分别是三角形ABC的BC，AC边上的高，
∴∠AEB=90°，∠ADB=90°，
∴在Rt△ABE中，G是斜边AB的中点，则GE=
AB．
同理，GD=
AB，
∴GD=GE．
又∵F是DE的中点，
∴GF⊥DE．
解：GF⊥DE．理由如下：如图，连接GE、GD．
∵AE，BD分别是三角形ABC的BC，AC边上的高，
∴∠AEB=90°，∠ADB=90°，
∴在Rt△ABE中，G是斜边AB的中点，则GE=
| 1 |
| 2 |
同理，GD=
| 1 |
| 2 |
∴GD=GE．
又∵F是DE的中点，
∴GF⊥DE．
点评：本题考查了直角三角形斜边上的中线、等腰三角形的判定与性质．解答该题时，充分利用了等腰△DGE的“三合一”的性质．
练习册系列答案
相关题目
