题目内容
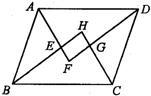53、（体验探究题）如图所示，已知在?ABCD中，各个内角的平分线相交于点E、F、G、H．（1）猜想EG与FH之间的关系；（2）试说明你猜想的正确性．
分析：因为平行四边形的邻角互补，则邻角的平分线组成的角为90°，有三个角是90°的四边形是矩形，故EG=FH．
解答：解：（1）EG=FH．
（2）证明：∵四边形ABCD是平行四边形，
∴∠BAD+∠ABC=180°．
又∵AF，BH分别平分∠BAD，∠ABC，
∴∠BAE+∠ABE=90°，
∴∠AEB=90°，
∴∠FEH=90°．
同理可证∠EFG=90°，∠EHG=90°，
∴四边形EFGH为矩形，
∴EG=FH．
（2）证明：∵四边形ABCD是平行四边形，
∴∠BAD+∠ABC=180°．
又∵AF，BH分别平分∠BAD，∠ABC，
∴∠BAE+∠ABE=90°，
∴∠AEB=90°，
∴∠FEH=90°．
同理可证∠EFG=90°，∠EHG=90°，
∴四边形EFGH为矩形，
∴EG=FH．
点评：此题主要考查平行四边形的性质和矩形的判定．
练习册系列答案
阅读快车系列答案
相关题目
6、（体验探究题）如图所示，该图中包含的平面图形有（ ）
25、（体验探究题）如图所示，已知一矩形ABCD中，AB=2BC，点E在边DC上，且AE=AB，则∠EBC的度数为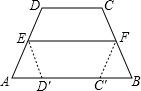
（体验探究题）如图所示，梯形ABCD中，DC∥AB，将梯形对折，使点D，C分别落在AB上的D′，C′处，折痕为EF，若CD=3cm，EF=4cm，则AD′+BC′的长为