题目内容
 平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为何?( )
平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为何?( )| A、110 | B、125 | C、130 | D、155 |
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
不等式组
的非负整数解有( )
|
| A、6个 | B、5个 | C、4个 | D、3个 |
 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A、CB=CD | B、∠BAC=∠DAC | C、∠BCA=∠DCA | D、∠B=∠D=90° |
 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )| A、∠B=∠C | B、∠BDA=∠CDA | C、AB=AC | D、BD=CD |
 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( )
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,射线AM、BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE、BN于点F、C,过点C作AM的垂线CD,垂足为D.若CD=CF,则
如图,射线AM、BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE、BN于点F、C,过点C作AM的垂线CD,垂足为D.若CD=CF,则| AE |
| AD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
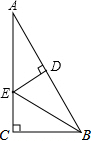 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于点D,若AB=6,则AE的值是( )
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于点D,若AB=6,则AE的值是( )A、3
| ||
B、2
| ||
| C、3 | ||
| D、2 |
 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是( )
如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是( )A、(
| ||
B、(
| ||
C、(
| ||
D、(
|

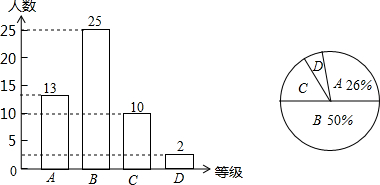 中A级:90~100分,B级:75~89分,C级:60~74分,D级:60分以下,则
中A级:90~100分,B级:75~89分,C级:60~74分,D级:60分以下,则