题目内容
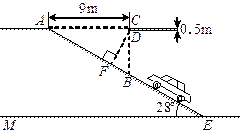
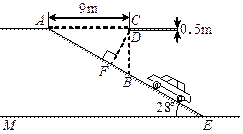
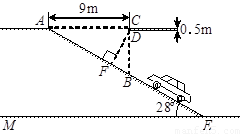
20、莱芜某大型超市为缓解停车难问题，建筑设计师提供了楼顶停车场的设计示意图．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．请根据如图，求出汽车通过坡道口的限高DF的长（结果精确到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．
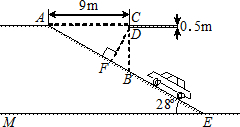
分析：根据锐角三角函数的定义，可在Rt△ABC中解得BC的值，进而求得BD的大小；在Rt△BDF中，利用余弦的定义，即可求得DF的值．
解答：解：在Rt△ABC中，∠A=28°，AC=9，
∴BC=ACtan28°≈9×0.53=4.77，
∴BD=BC-CD=4.77-0.5=4.27，
∴在Rt△BDF中，∠BDF=∠A=28°，BD=4.27，
∴DF=BDcos28°≈4.27×0.88=3.7576≈3.8，
答：坡道口的限高DF的长是3.8m．
∴BC=ACtan28°≈9×0.53=4.77，
∴BD=BC-CD=4.77-0.5=4.27，
∴在Rt△BDF中，∠BDF=∠A=28°，BD=4.27，
∴DF=BDcos28°≈4.27×0.88=3.7576≈3.8，
答：坡道口的限高DF的长是3.8m．
点评：本题考查了解直角三角形的应用，坡面坡角问题和勾股定理，解题的关键是坡度等于坡角的正切值．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
